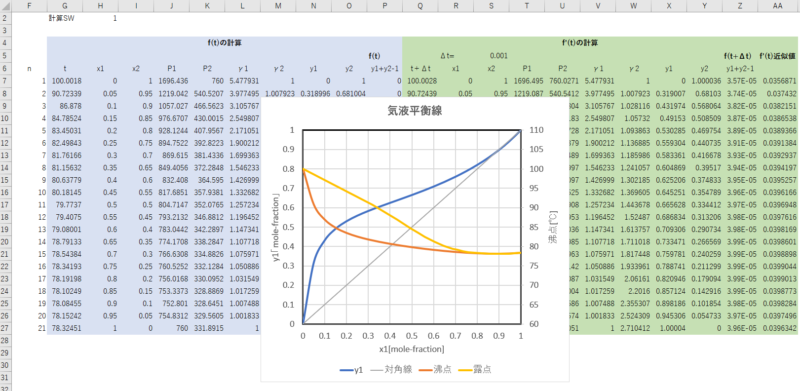
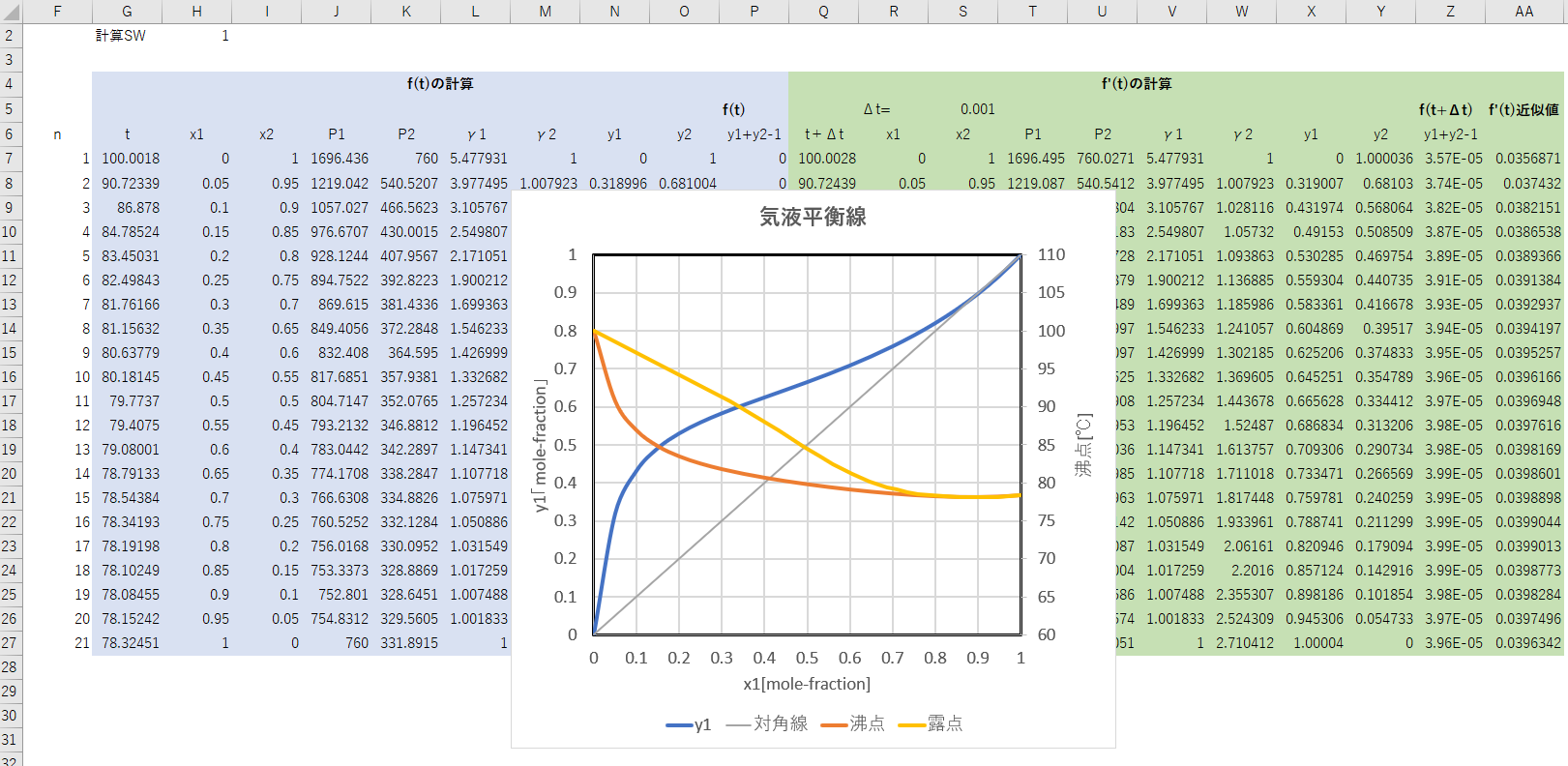
上の図は、Excelで計算したエタノール(1)-水(2)系の非理想系気液平衡図です。
気液平衡の計算は、蒸留の基礎となるものです。
ここでは、Excelを使った気液平衡計算を紹介します。
1. 理想系気液平衡計算
次の系でExcelによる理想系の気液平衡計算を紹介します。
ベンゼン(1)- トルエン(2)二成分系
ベンゼン液組成(モル分率) 0~1 (0.05刻み)
全圧 \(\pi = 760 \, \text{mmHg}\)
蒸気圧 Antoine式
\(\log(P_i) = A_i – \frac{B_i}{t + C_i} \text{ 単位:}\ P_i\ [\text{mmHg}], t\ [^\circ C]\)
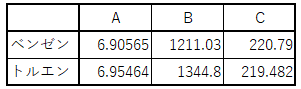
出典 化学工学協会編:「改訂五版 化学工学便覧」,丸善,(1988)
1-1 気液平衡の計算式
気液平衡計算の基本式は次の通りです。
\(y_1 = \frac{P_1}{\pi} x_1\)
\(y_2 = \frac{P_2}{\pi} x_2\)
\(y_1 + y_2 = 1\)
これらの式を用いて、与えられた液組成から沸点を求めることが気液平衡計算です。そのため、以下の非線形方程式を解く必要があります。
\(f(t) = \frac{10^{(A_1 – \frac{B_1}{t + C_1})}}{\pi} x_1 + \frac{10^{(A_2 – \frac{B_2}{t + C_2})}}{\pi} x_2 – 1 = 0\)
1-2 ニュートン-ラプソン法
ニュートン・ラプソン法は、非線形方程式の近似解を求めるための数値解法の一つです。
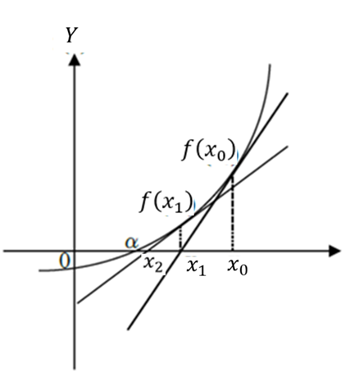
解き方は、次の手順で進めます。
- 解を求める方程式 \( f(x)=0\)で初期値\(x_0\)とし、\(f(x_0)\)と\(f’(x_0)\)を計算します。
- 新しい\(x_1 = x_0 – \frac{f(x_0)}{f'(x_0)}\)を計算します。
- この\(x_1\)を使って\(f(x_1),f’(x_1)\)を計算します。
- これを繰り返し\(f(x)\)が十分にゼロに近づいたところが解となります。
1-3 ニュートン-ラプソン法による気液平衡計算
STEP1
まず最初に、Antoine定数、全圧を入力します。
次に、\(x_1=0.5, x_2=0.5\) の場合の沸点計算から始めます。初期値として\( t\) の値を 100℃ に設定し、\(f(t) = y1 + y2 – 1\) を計算します。

STEP2
\(f(t)\) の導関数\( f'(t)\) を求めます。導関数は以下のように求められます。
\(f'(t) = \frac{10^{A_1 – \frac{B_1}{t + C_1}} \cdot \frac{B_1}{(t + c_1)^2} \ln{10}}{\pi} x_1 + \frac{10^{A_2 – \frac{B_2}{t + C_2}} \cdot \frac{B_2}{(t + c_2)^2} \ln{10}}{\pi} x_2\)
STEP3
この計算式を新たに、ワークシートに加えます。ここでは式が長いため3列を使用しています。
得られた\(f(t)\)と\(f’(t)\)から新たな沸点を求めます。
\(t_{n+1} = t_n – \frac{f(t_n)}{f'(t_n)}\)

STEP4
最後に、G列とH列からQ列を下にコピーして、気液平衡計算を完成させます。
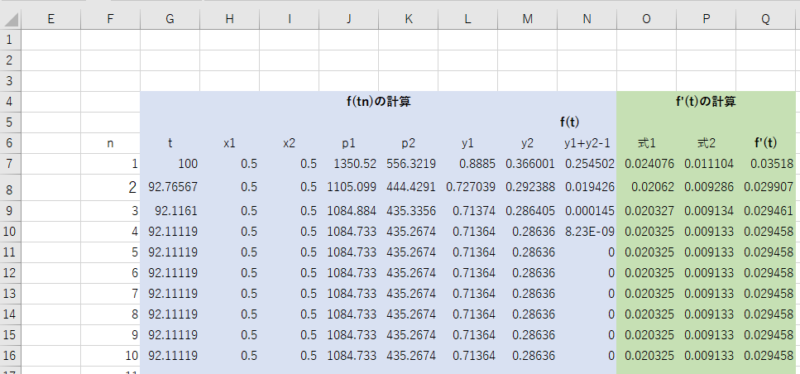
この計算を5回繰り返すことで近似解が得られます。初期値(G7)を変更して計算すると、初期値と収束回数の関係がわかります。
1-4 近似計算による微分値の使用
ニュートン-ラプソン法では、微分値(導関数)を求める必要があります。気液平衡計算では導関数を比較的容易に求めることができますが、導関数の計算に時間がかかる場合もあります。
ここでは、次の近似式による微分値を使った計算を紹介します。
\(f'(x_n) \approx \frac{f(x_{n+\Delta x}) – f(x_n)}{\Delta x}\)
STEP1
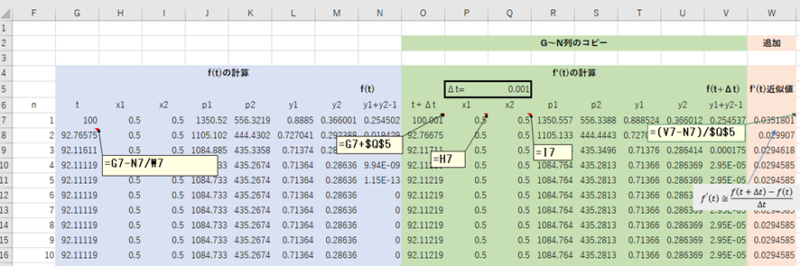
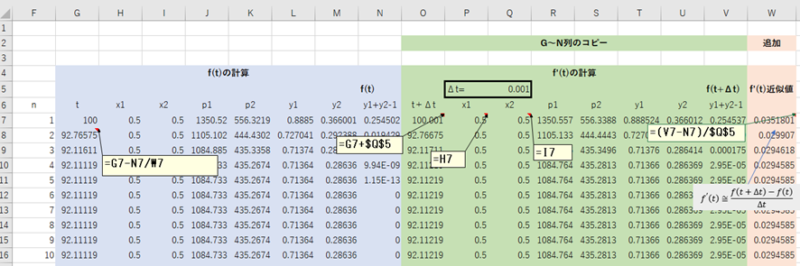
- 微分値を計算したO,P,Q列を削除
- G~N列をO~V列にコピー
- Q5をΔtとして0.001を入力し、下にコピー
- O7に=G7+$Q$5を入力し、下にコピー(t+Δt)
- P7に=H7を入力し、下にコピー
- Q7に=I7を入力し、下にコピー
- W5に” f'(t)近似値”を入力
- W7に=(V7-N7)/$Q$5を入力し、下にコピー
- G8に=G7-N7/W7を入力し、下にコピー
STEP2
この変更により、微分値の近似値を使用した計算が行えます。微分値を使用する場合とあまり変らないことがわかるでしょう。
1-5 1行で計算する
これで気液平衡計算は出来たわけですが、\(x_1\)を0~1(0.05刻み)計算しグラフにするためには、1行でこの計算を完結させるのが便利です。
反復計算を使い1行で計算出来るようにします。
STEP1
まず準備として、ファイル→オプション→数式を選択してください。すると、次の表示が出てきます。
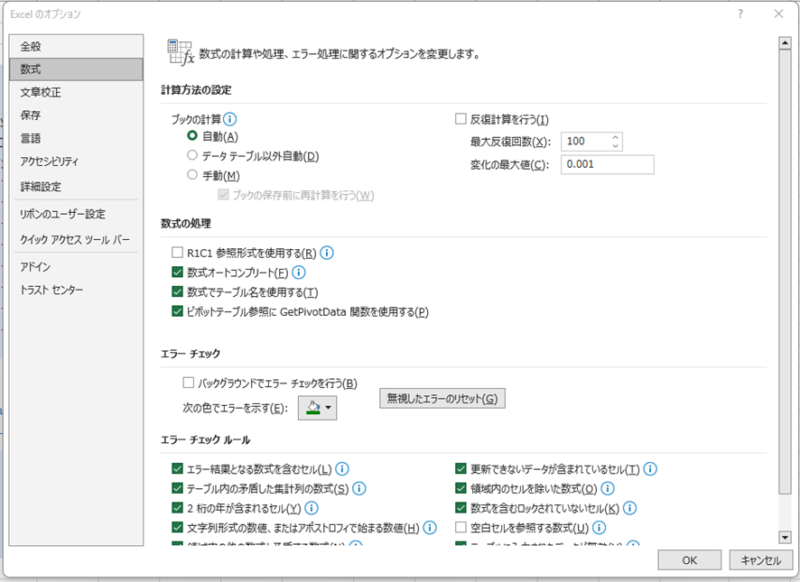
ここで、右上の反復計算を行うにチェックを入れ、OK ボタンをクリックしてください。
STEP2
次に、G7に = G7 – N7 / W7 を入力します。これにより、1行で計算が行われることが分かるでしょう。
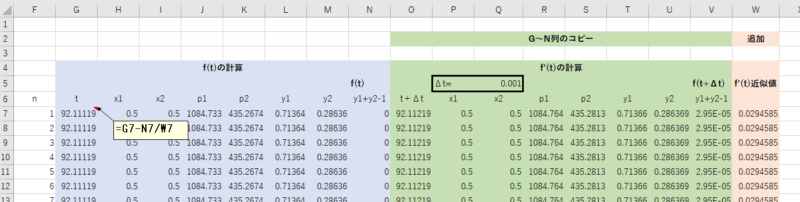
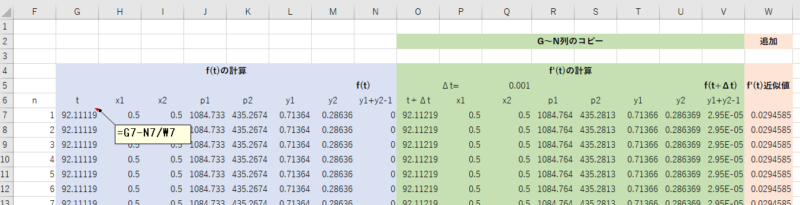
G7の式に G7 を含むと言う矛盾があるように見えますが、”反復計算を行う” オプションが有効になっているため、G7 は前回の計算値を指します。
STEP3
エラーが発生した場合に回復できないため、H2に計算SWを設定し、計算SW=0の場合は初期値を100に設定するようにしておくことをお勧めします。
G7の式: = IF($H$2=0, 100, G7 – N7/W7)
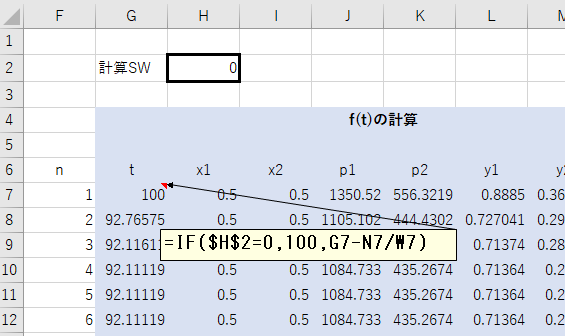
さらに、行数を増やして\( x_1\) を0から1まで0.05刻みで変化させ、気液平衡曲線(\(x-y\)図、沸点-露点曲線)を作成することができます。
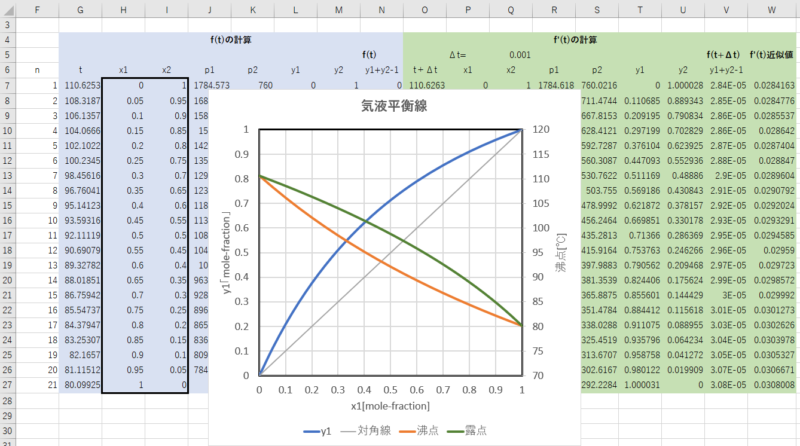
2. 非理想系気液平衡計算
次の系でExcelによる非理想系の気液平衡計算を紹介します。
水(1)- エタノール(2)二成分系
エタノール液組成(モル分率) 0~1 (0.05刻み)
全圧 \(\pi = 760 \, \text{mmHg}\)
蒸気圧 Antoine式
\(\log(P_i) = A_i – \frac{B_i}{t + C_i} \text{ 単位:}\ P_i\ [\text{mmHg}], t\ [^\circ C]\)
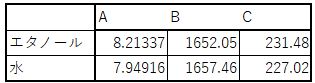
出典 化学工学協会編:「改訂五版 化学工学便覧」,丸善,(1988)
2-1. 非理想系気液平衡の計算式
非理想系の気液平衡計算の基礎式は次の通りです。
\(y_i = \frac{p_i}{\pi} x_i \gamma_i\)
理想系の気液平衡計算の基礎式\(y_i = \frac{p_i}{\pi} x_i\)に活量係数\(\gamma_i\)を導入したものになっています。この\(\gamma_i\)を液側活量係数と言い、溶液中の成分間の相互作用を表す重要なパラメータで、液組成、温度の関数になっています。
この液側活量係数を計算するためにはNRTL式、Wilson式などの様々なモデルがあります。ここでは、Wilson式を使って計算を進めていきます。
2-2. Wilson式
Wilson式は、液相活量係数\(γ_i\)を次のように計算します。
\(\ln(\gamma_i) = 1 – \ln\left(\sum_{j=1}^N x_j \Lambda_{ij}\right) – \sum_{k=1}^N \frac{x_k \Lambda_{ki}}{\sum_{j=1}^N x_j \Lambda_{kj}}\)
\(\Lambda_{ij} = \frac{V_j^L}{V_i^L} \exp\left(-\frac{\lambda_{ij} – \lambda_{ii}}{RT}\right)\)
温度依存性を考慮しなければ、\(\Lambda_{12}, \Lambda_{21}\)2つのパラメータとなります。
また、2成分系に限定すれば次の式となります。
\(\ln(\gamma_1) = -\ln\left(x_1 + x_2 \Lambda_{12}\right) + x_2 \left(\frac{\Lambda_{12}}{x_1 + x_2 \Lambda_{12}} – \frac{\Lambda_{21}}{x_1 \Lambda_{21} + x_2}\right)\)
\(\ln(\gamma_2) = -\ln\left(x_2 + x_1 \Lambda_{21}\right) – x_1 \left(\frac{\Lambda_{12}}{x_1 + x_2 \Lambda_{12}} – \frac{\Lambda_{21}}{x_1 \Lambda_{21} + x_2}\right)\)
パラメータ \(\Lambda_{12}, \Lambda_{21} \quad (\Lambda_{11} = 1, \Lambda_{22} = 1)\)
2-3. 非理想系の気液平衡計算
非理想系の気液平衡計算に移ります。
Excelは、理想系気液平衡計算で作成した最終のシートを使います。
Step1
このシートで成分名、Antoine定数を書き換え、Wilsonパラメータを追加します。
\(\Lambda_{12} = 0.2223, \quad \Lambda_{21} = 0.8028\)
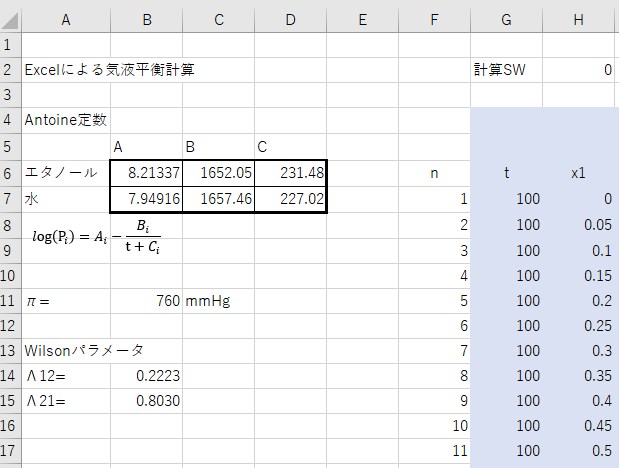
計算SWもゼロとしておきます。
Step2
活量係数を計算するため、P2とy1の間に2列挿入し、γ1,γ2とします。
この列に\(\gamma_1\),\(\gamma_2\)の計算式を入力し、y1,y2の計算式にも\(\gamma\)を追加します。
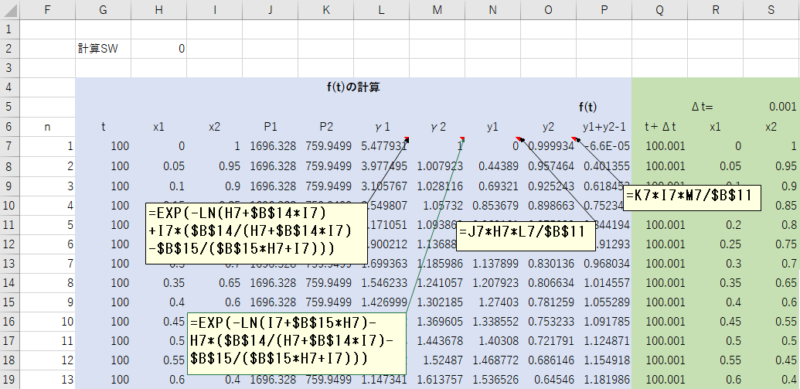
Step3
γ1,γ2及びy1,y2の計算式をf’(t)の計算にもコピーします。
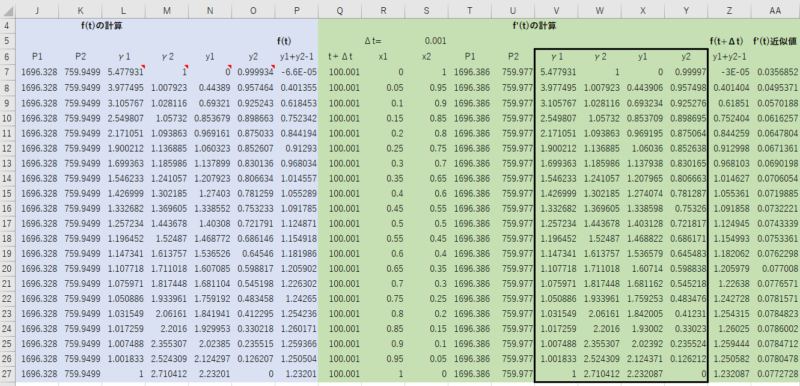
Step4
ここで、計算SW=1にすると非理想系の気液平衡計算が計算されます。
これで完成です。