蒸留計算では蒸留塔の各段の組成、温度を計算します。
この動画は、ここで紹介するトリダイアゴナル法による蒸留計算のデモです。デモのため、収束に時間を掛けていますが、実際はより短い時間で収束します。
1.蒸留計算法
蒸留計算法には二つのアプローチがあります。
一つはフィード流量、フィード組成、製品組成、還流比を与え、必要な理論段数を求める方法です。これは設計型の問題であり、有名なMcCabe-Thiele法がこれに該当します。
もう一つは、フィード流量、フィード組成、還流比、理論段数などを与え、製品組成を含む塔内の組成分布や温度分布を求める方法です。これは操作型の問題であり、コンピュータを使用した計算が主にこれに該当します。
ここでは、蒸留塔の物質収支式から連立方程式を導出し、それを行列計算で解くトリダイアゴナル法を紹介します。
参考 平田光穂(監修), 佐野 司朗(編), “JACEデザインマニュアルシリーズ 蒸留(第1巻)”,
ジェイス・リアサーチセンター(1978)
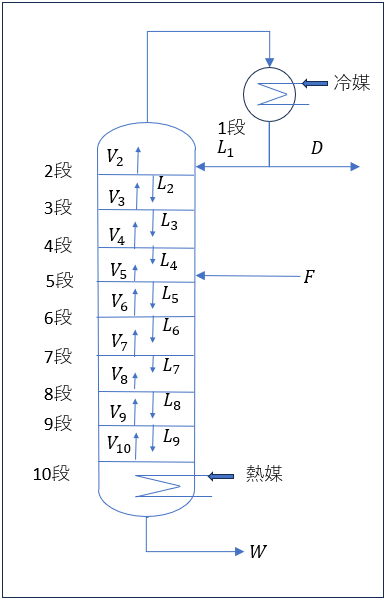
1-1.連続蒸留塔の例
コンデンサー、リボイラーを含め理論段数10段でベンゼン(1)-トルエン(2)の2成分の分離を行う蒸留塔を例として使用します。
下記の仮定のもと計算を行います。
下記の仮定のもと計算を行います。
- 各成分のモル蒸発潜熱は等しく、従って各段の蒸気量液量は濃縮部、回収部で一定とします。
- フィード液は、沸点の液体で供給され、従って濃縮部、回収部の蒸気量は同じとなります。
操作条件
- フィード(F) \(10kmole/h\)
- フィード組成 \(x_{F,1}=0.5, x_{F,2}=0.5\)
- 留出量(D) \(5kmole/h\)
- 還流流量 \(20kmole/h\)
- 圧力 \(760mmHg\)
- フィード段 \(5\)
液量と蒸気量の関係
- \(V_2 = L_1 + D\)
- \(V_2=V_3=V_4=V_5=V_6=V_7=V_8=V_9=V_{10}\)
- \(L_1 = L_2 = L_3 = L_4 = L_5\)
- \(L_5 + F = L_6 = L_7 = L_8 = L_9\)
2. トリダイアゴナル法
2-1. 物質収支式
各段の物質収支式は次のようになります。
- \(V_2 \cdot y_{2,i} – L_1 \cdot x_{D,i} – D \cdot x_{D,i} = 0\)
- \(V_3 \cdot y_{3,i} + L_1 \cdot x_{D,i} – V_2 \cdot y_{2,i} – L_2 \cdot x_{2,i} = 0\)
- \(V_4 \cdot y_{4,i} + L_2 \cdot x_{2,i} – V_3 \cdot y_{3,i} – L_3 \cdot x_{3,i} = 0\)
- \(V_5 \cdot y_{5,i} + L_3 \cdot x_{3,i} – V_4 \cdot y_{4,i} – L_4 \cdot x_{4,i} = 0\)
- \(V_6 \cdot y_{6,i} + L_4 \cdot x_{4,i} – V_5 \cdot y_{5,i} – L_5 \cdot x_{5,i} = – F \cdot x_{F.i} \)
- \(V_7 \cdot y_{7,i} + L_5 \cdot x_{5,i} – V_6 \cdot y_{6,i} – L_6 \cdot x_{6,i} = 0\)
- \(V_8 \cdot y_{8,i} + L_6 \cdot x_{6,i} – V_7 \cdot y_{7,i} – L_7 \cdot x_{7,i} = 0\)
- \(V_9 \cdot y_{9,i} + L_7 \cdot x_{7,i} – V_8 \cdot y_{8,i} – L_8 \cdot x_{8,i} = 0\)
- \(V_{10} \cdot y_{10,i} + L_8 \cdot x_{8,i} – V_9 \cdot y_{9,i} – L_9 \cdot x_{9,i} = 0\)
- \(L_9 \cdot x_{9,i} – V_{10} \cdot y_{10,i} – W \cdot x_{W,i} = 0\)
方程式が10個に対し、未知数は\(x_{D,i},x_{2,i}-x_{9,i},x_{W,i},y_{2,i}-y_{10,i}\)と19個有りこのままでは解くことは出来ません。
そこで\(x_{n,i}\)に初期値(通常はフィード液組成)を入れ、気液平衡関係から\(y_{n,i}\)を求め、 \(K_{n,i} = \frac{y_{n,i}}{x_{n,i}}\) を計算します。
\(y_{n,i}\)を\(y_{n,i} = K_{n,i} \cdot x_{n,i}\)とすることにより、未知数を10個に減らすことが出来ます。これで、連立方程式が解け\(x_{n,i}\)が求まるわけです。
しかし、新しい\(x_{n,i}\)では\(K_{n,i}\)の値は変ってしまいます。そこで新しい\(K_{n,i}\)を使って再び\(x_{n,i}\)を求めるわけです。
これを繰り返し行い、\(x_{n,i}\)が変化しなくなり、物質収支を満足させた時を解とします。
2-2. 行列による解法
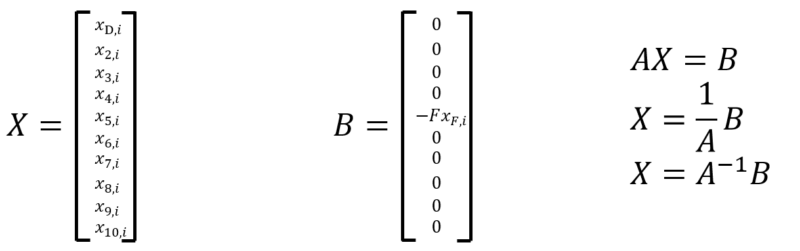
ここでは、下記の行列計算を行うことにより、解を求めています。
Excelでは、行列積はMMULT(行列1 ,行列2 )、逆行列はMINVERSE(行列)で計算出来るため、連立方程式は簡単に解が求まります。
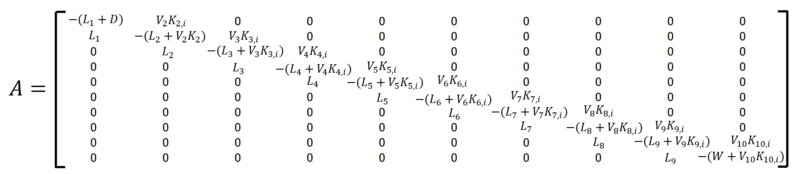
2-3. Excelでのトリダイアゴナル法の計算
STEP1
理想系気液平衡計算で作成した最終のブックを使います。
このブックに新しくシートを追加し、名前を”計算”とします。理想系気液平衡計算のシートは”気液平衡計算”とします。
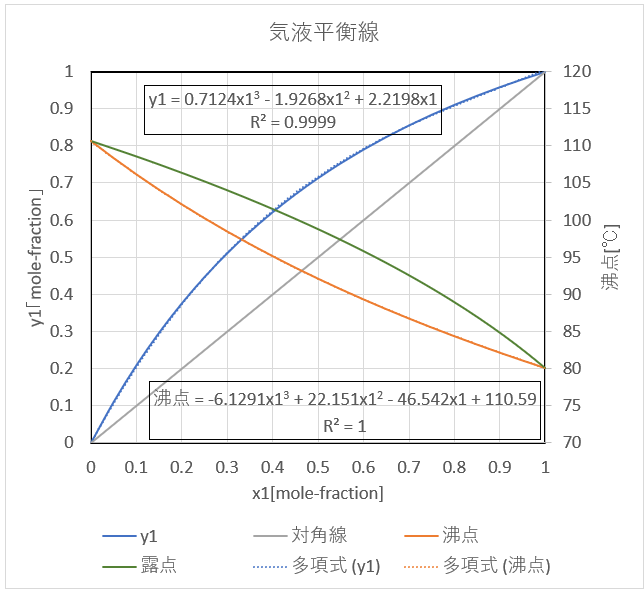
気液平衡の簡易的な計算方法として、\(y_{i}\)と\(T\)を表す\(x_{i}\)の多項式を作り、これから計算する方法もあります。
STEP2
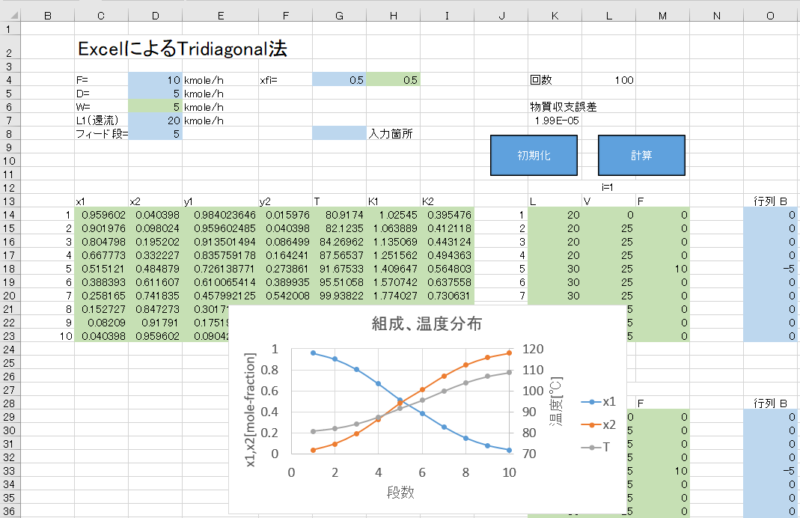
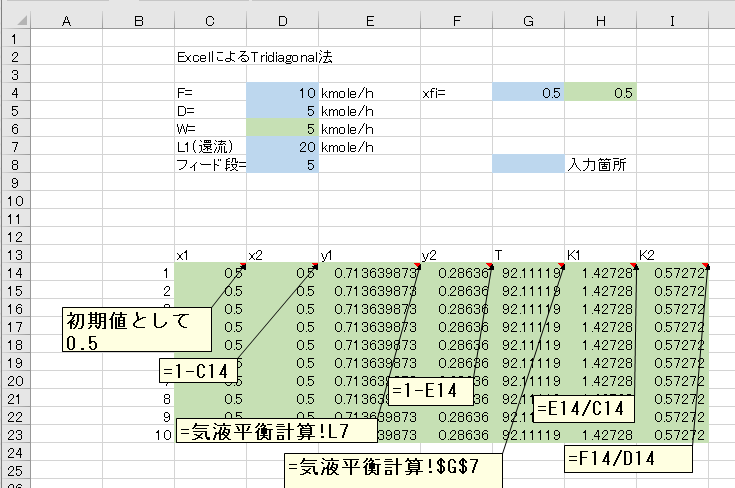
“計算”シートに操作条件を入力します。
更に、14行目にx1,x2,y1,y2,T,K1,K2の数式を入力し、23行までコピーします。
STEP3
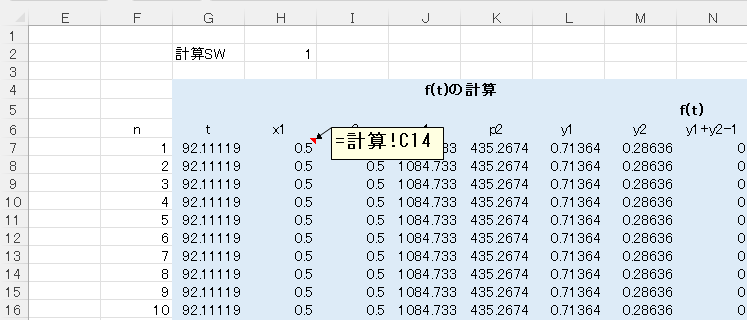
“気液平衡計算”シートでは、x1に”計算”シートのx1を設定します。
STEP4
これ以降は、”計算シート”での作業になります。
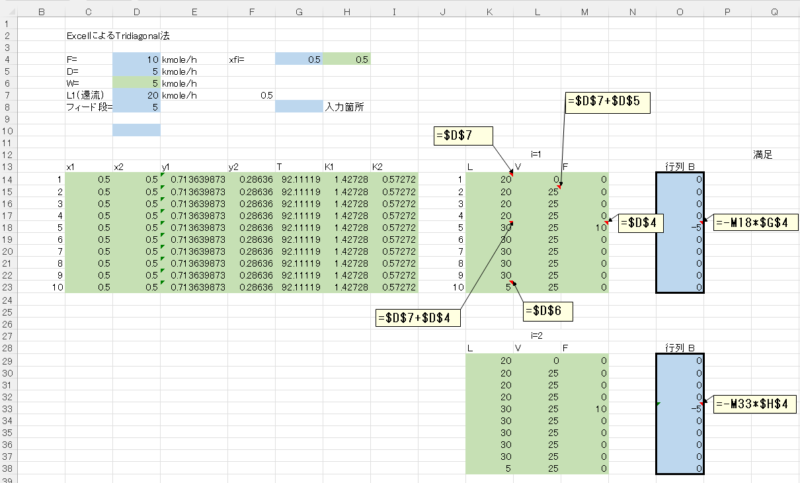
L,V,Fに各段の流量を入力し、行列Bでフィード段に \(-F\cdot x_{F,i}\) を入力します。
STEP5
次に、行列Aを入力します。 行列Aの緑色、黄色、青色の部分は、段数が1つずつ増えている形になっているため、最初の式をコピーして入力できます。 その後、赤色と灰色の部分を入力します。
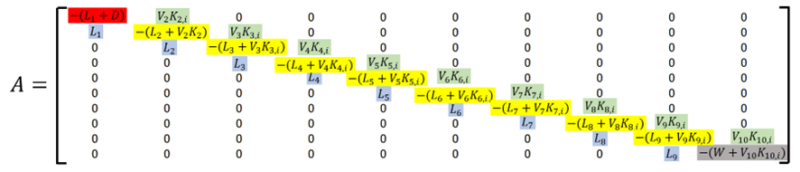
Excelでは次の通りです。

STEP6
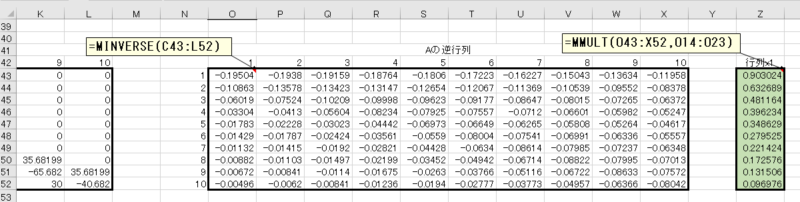
行列Aが出来たので、行列計算で \(x_{n,i}\) を計算します。
\([X] = [A]^{-1} [B]\)
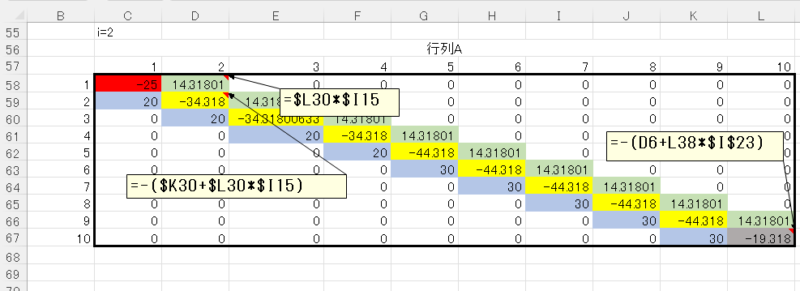
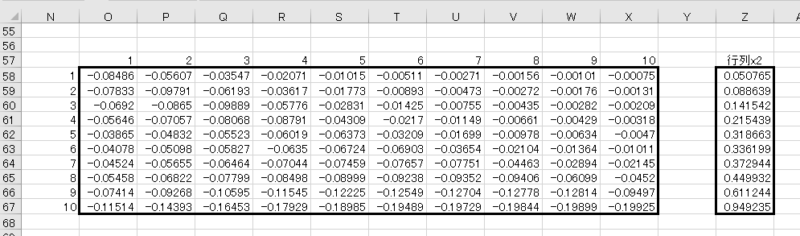
STEP7
同様にi=2についても計算します。
STEP8
ここで求めた \(x_{n,i}\) では \(x_{n,1} + x_{n,2} = 1\) になりません。
そこで正規化します。
\(\frac{x_{n,1}}{x_{n,1} + x_{n,2}}, \frac{x_{n,2}}{x_{n,1} + x_{n,2}}\)
これを新しい \(x_{n,i}\) とした場合、変動が激しく発散する可能性があります。
このためファクタ \(\alpha\) を使い補正します。
新しい \(x_{n,i}=\) 前の \(x_{n,i}+\) (計算した \(x_{n,i}-\) 前の \(x_{n,i})\alpha\)
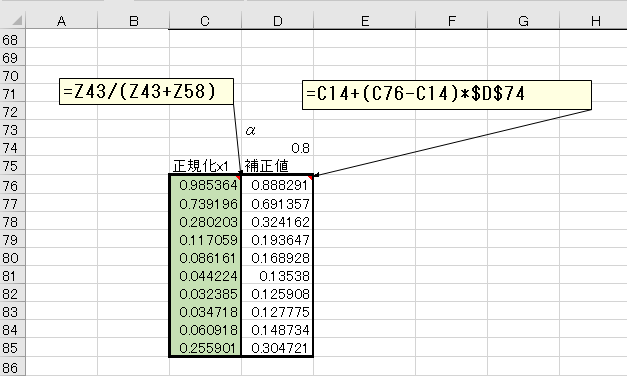
STEP9
物質収支の確認は、各段、全体で行います。
例を示します。
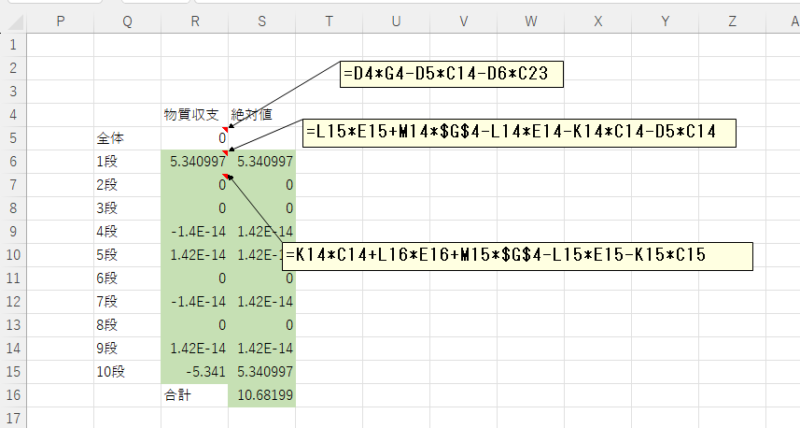
STEP10
求めた新しい \(x_{n,i}\) を、初期値の代わりに入力します。
具体的には、D76:D85をコピーし、これをC14に値貼付けします。
これをマクロにより繰り返すことにより、収束解が得られます。
これがマクロです。L4に回数を設定することにより、その回数だけ繰り返します。
尚、マクロを実施する前に保存しておいて下さい。
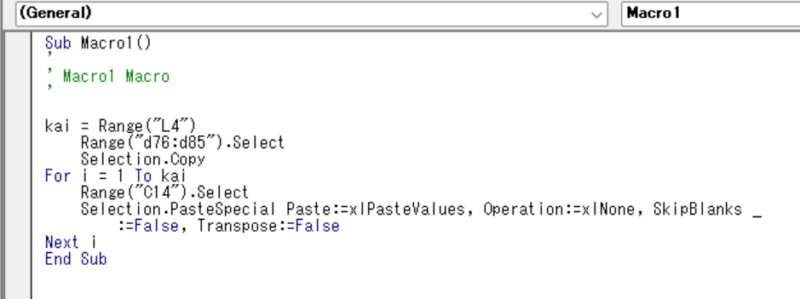
これが、100回繰り返したときの計算結果です。