”Excelによる反応計算1 CSTR”を変更した”Excelによる反応計算2 バッチ反応器”を先に紹介しました。
今回は、”Excelによる反応計算2 バッチ反応器”をさらに変更したセミバッチ反応器の反応計算を紹介します。
なお、バッチ反応器のExcelシートの変更になります。
バッチ反応器のExcelシートをお持ちの方は、セミバッチ反応器での変更箇所とある部分を変更入力することにより完成します。
目次
1.バッチ反応器の例
下記の仮定のもと計算を行います。
- 液相反応とし反応に伴う密度変化がない。
操作条件
- 量論式、反応速度式
- \(\text{A + B} \rightarrow \text{C} \quad r_1 = k_1 C_A C_B\quad k_1=1.0\)
- \(\text{C} \rightarrow \text{D} \quad r_2 = k_2 C_C\quad k_2=3.0\)
- \(\text{A +C} \rightarrow \text{E} \quad r_3 = k_3 C_A C_C\quad k_1=0.5\)
- 単位 \(r_n : kmol / m^3 ・ hr , C_i : kmol / m^3 \)
- 操作方法 セミバッチ反応器での変更箇所
- 原料Bを反応器に仕込み、原料Aを連続でフィードする。
- 仕込み原料 セミバッチ反応器での変更箇所
- 体積 \(0.5 \, \text{m}^3\)
- 濃度 \(C_{A0} = 0.0 , C_{B0}=10.0 , C_{C0} = 0.0 , C_{D0}=0.0 , C_{E0} = 0.0\) \(kmol / m^3\)
- フィード原料 セミバッチ反応器での変更箇所
- 体積流量 \(0.125 \, \text{m}^3/hr\)
- 濃度 \(C_{A0} = 12.0 , C_{B0}=10.0 , C_{C0} = 0.0 , C_{D0}=0.0 , C_{E0} = 0.0\) \(kmol / m^3\)
- 4hrフィード
2.物質収支式
各成分の物質収支式は非定常状態とすると次の様になります。
- \(\frac{dn_A}{dt} = vC_{A0} + r_1 V + r_2 V + r_3 V – vC_A = vC_{A0} + k_1 C_A C_B V + k_2 C_C V + k_3 C_A C_C V – vC_A \)
- \(\frac{dn_B}{dt} = vC_{B0} + r_1 V + r_2 V + r_3 V – vC_B = vC_{B0} + k_1 C_A C_B V + k_2 C_C V + k_3 C_A C_C V – vC_B \)
- \(\frac{dn_C}{dt} = vC_{C0} + r_1 V + r_2 V + r_3 V – vC_C = vC_{C0} + k_1 C_A C_B V + k_2 C_C V + k_3 C_A C_C V – vC_C \)
- \(\frac{dn_D}{dt} = vC_{D0} + r_1 V + r_2 V + r_3 V – vC_D = vC_{D0} + k_1 C_A C_B V + k_2 C_C V + k_3 C_A C_C V – vC_D \)
- \(\frac{dn_E}{dt} = vC_{E0} + r_1 V + r_2 V + r_3 V – vC_E = vC_{E0} + k_1 C_A C_B V + k_2 C_C V + k_3 C_A C_C V – vC_E \)
この微分方程式をオイラー法で数値積分することにより、定常解を得ることが出来ます。
3. Excelによる回分反応器の計算
この例では、反応が違っても対応できるよう次のようにしています。(前に紹介した”Excelによる反応計算1 CSTR”に同じ)
- 複数の反応(最大4)に対応できる、
- 最大6成分に対応できる。
- 物質収支の計算式の変更を不要とするため、反応の量論係数、反応次数、反応速度定数を入力する方法とする。
3-1. 反応の定義
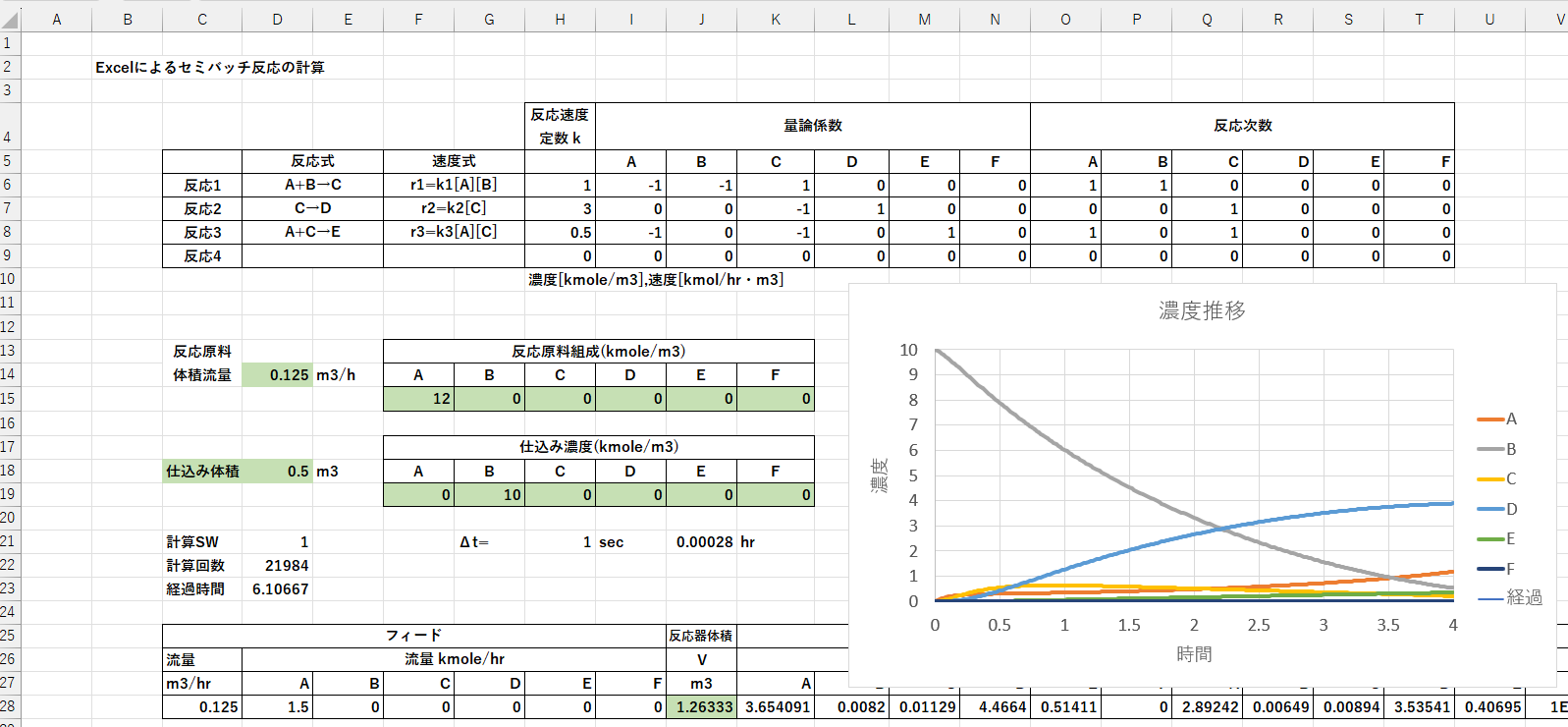
反応1~4に、下記項目を入力します。
- 反応式、速度式を入れます。これは、分かりやすくするためで特に計算には関係しません。
- 反応速度定数を入力します。(H6~H9)
- 量論係数を入力します。原料側はマイナスとなります。(I6~N9)
- 反応次数を入力します。(O6~T9)
3-2. 原料供給、反応器体積
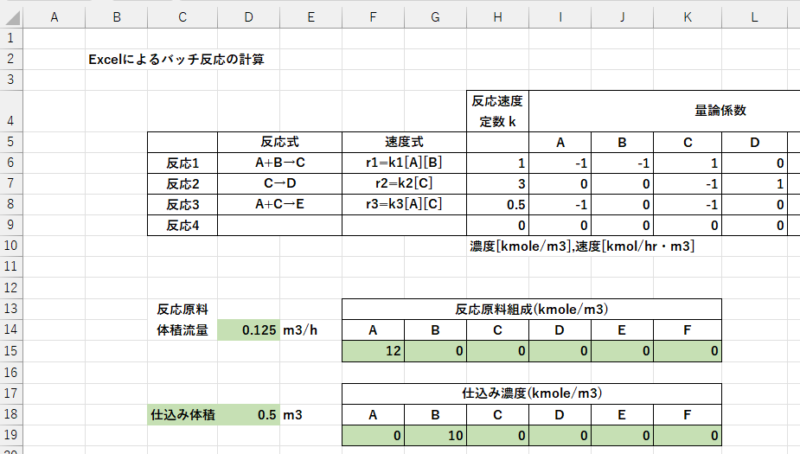
- 反応原料体積流量を入力します。(D14) セミバッチ反応器での変更箇所
- 反応原料組成を入力します。(F15~K15) セミバッチ反応器での変更箇所
- 仕込み体積(反応器体積を変更)を入力します。(D18) セミバッチ反応器での変更箇所
- 仕込み濃度を入力します。(F19~K19) セミバッチ反応器での変更箇所
3-3. 反復計算、数値積分の設定
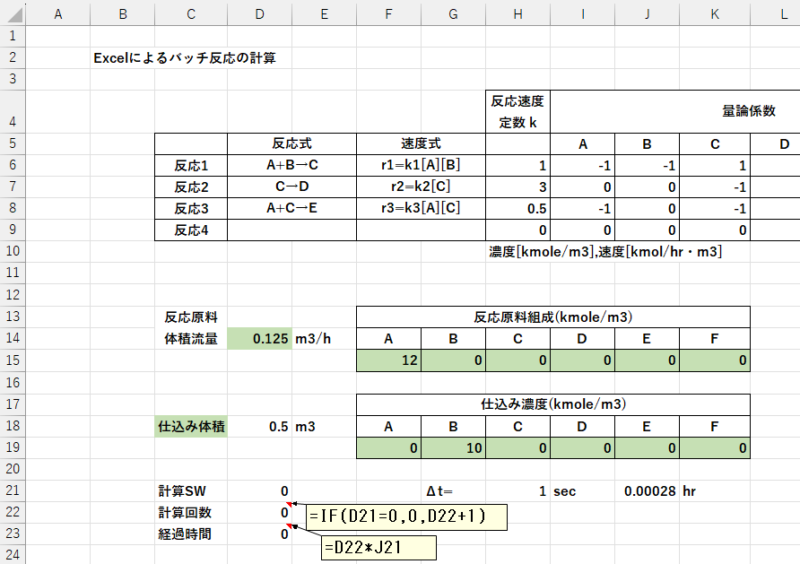
- ここでも反復計算を使うので、計算SWを入力します。(D21)
- 計算回数、経過時間も計算させます。(D22,D23)
- 数値積分の刻み幅(Δt)を入力します。(H21)
CSTRでは、最終の定常解が必要でしたが、バッチ反応器では途中の計算結果が重要になるため、(Δt)は小さくする必要があります。
3-4. 反応計算(1)
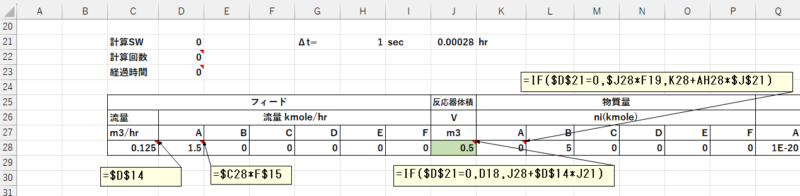
- 反応原料の体積流量の式を入力します。(C28)
- 反応原料の流量の式を入力します。(D28,I28)
- 仕込み体積(=反応器体積)の式を入力します。(J28) セミバッチ反応器での変更箇所
- 反応器内の物質量の式を入力します。(K28)
- 計算SW($D$21)が0の時は、仕込み体積(\J28)×仕込濃度(F$19)となります。
- 計算SW($D$21)が0以外の時は、現在の値(K28)に\(\frac{dn_A}{dt}\) (AH28)×Δt($J$21)を加えた値となります。
3-4. 反応計算(2)
- 濃度の式を入力します。(Q28)
- 濃度は、次の反応量計算でべき乗されるため、0ではエラーとなります。
- このため、物質量(K28)が0の時は、0でない小さな数値(1e-20)としています。
- 反応別反応量の式を入力します。(W28)
- \(r_1 V = k_1 C_A^l C_B^m C_C^n C_D^o C_E^p C_F^q V\)

3-4. 反応計算(3)
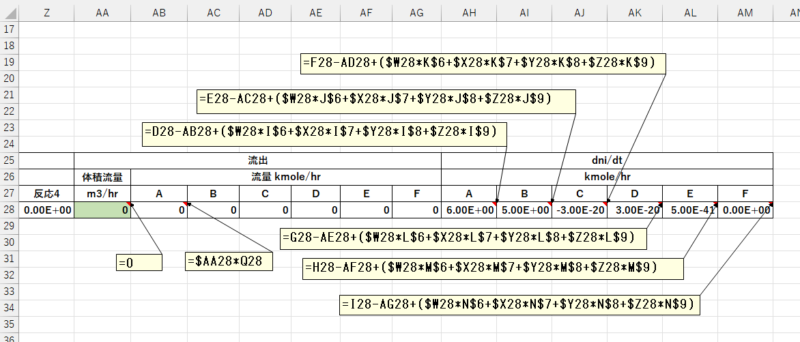
- 流出の体積流量はゼロとなりますから、AA28は0を入力します。 セミバッチ反応器での変更箇所
- 流出の流量の式を入力します。(AB28,AG28)
- \(\frac{dn_A}{dt}\) の式を入力します。(AH28)
- \(\frac{dn_A}{dt} = v C_{A0} – v C_A+r_1 a_1 + r_2 a_2 + r_3 a_3 + r_4 a_4\)
- \(a_1\)~\(a_4\)は、反応1~4の量論係数を表します。
3-5. 反復計算の設定
この計算でも反復計算を使用します。
ファイル → オプション → 数式 で、下記画面を出します。
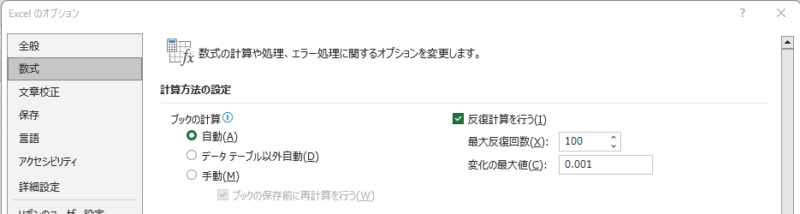
最大反復回数を入力し、反復計算を行うにチェック入れてOKを押せば、反復計算を行います。
反復回数は計算したい時間/Δtとなります。
反復回数の最大値は10,000回のため、それ以上の場合はファンクションキーF9を押し再度反復計算させます。
3-6. 途中経過の記録
バッチ反応器では、途中の経過が重要となります。
ここでは、反復計算を利用して途中経過の記録を行います。
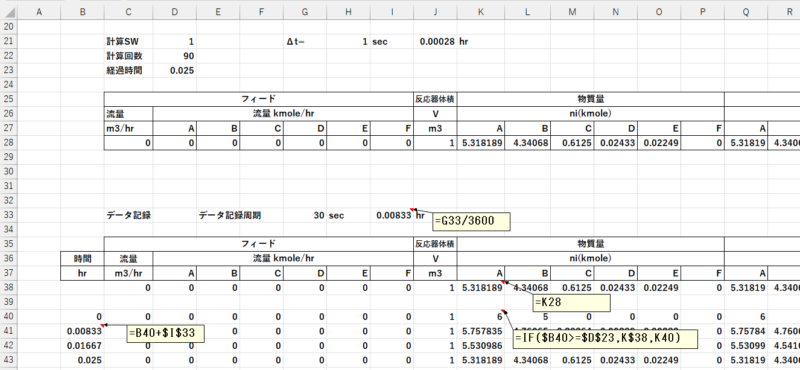
物質量A(K28)を記録する場合で説明します。
- K38に=K28と設定し、物質量Aを表示します。
- G33に記録する周期を入力します。この場合は30secとなり、I33でhrに変換されます。
- B40に0を入力し、B41に=B40+$I$33と設定し、記録したい時間分だけ下にコピーします。
- K40に下記式を設定し、下にコピーします。
- =IF($B40>=$D$23,K$38,K40)
- この式の意味は、記録を残したい時刻($B40)が現在の経過時間($D$23)より大きい場合、すなわちまだその時間になっていない場合は、現在の値(K$38)とし、経過時間以上になったら、現在表示している値(K40)をそのまま保持します。
これにより、その時間の値を記録することが可能となります。
3-7. Excelによる反応計算 バッチ反応器の完成
以上により、Excelによる反応計算3 セミバッチ反応器が完成します。
なお、本計算方法はオイラー法のため刻み幅により精度が落ちる場合があります。刻み幅の選定には注意が必要です。
(ルンゲ・クッタ法に変更することにより改善されます。)