“ExcelによるPID制御のチューニング(3)設定値変更データを用いる方法(1)”で紹介した方法について、今回は具体的なExcelにより計算を紹介します。今回は、比例微分先行PID制御(I-PD制御)です。
尚、前回は、PV値の参照モデルとの一致を評価してP,I,Dパラメータの最適化を行う方法と紹介しましたが、後半では、OP値の変動も最適化の目的関数に含めて紹介します。
この方法は、下記の資料の“E-FRIT法”を参考にしています。
加納,小河,田坂,高橋,滝波,吉井,大寶,増田:モデル不要PID調整法E-FRITの開発と実用化,計測と制御,50–12,1076/1079 (2011)
今回紹介するのは、PV値の参照モデルとの一致を評価してP,I,Dパラメータの最適化を行う方法です。チューニングの手順
チューニングの手順は次の通りになります。
- 設定値変更データの入手
\(SP\),\(PV\),\(OP\)、P,I,Dパラメータ、PID調節計の種類(PI-D,I-PD) - 整定時間の決定
- P,I,Dパラメータおよび参照モデルの無駄時間の仮定
- PID調節計種類、整定時間及び無駄時間から参照モデルの時定数の決定
- P,I,Dパラメータ及び\(OP\)から\(\overline{SP}\)を計算
- \(\overline{SP}\)から参照モデルを使い\(\overline{PV}\)を計算
- \(\Sigma(PV-\overline{PV})^2\)を計算
- \(\Sigma(PV-\overline{PV})^2\)が十分小さければ最適P,I,Dパラメータ、十分小さくなければ3.に戻る
2.Excelでのチューニング
2-1.使用する設定値変更データ
ここでは、”ExcelによるPID制御のシミュレーション(2)”で作成したExcelシート(定位型)を使用し、設定値変更データを作成します。
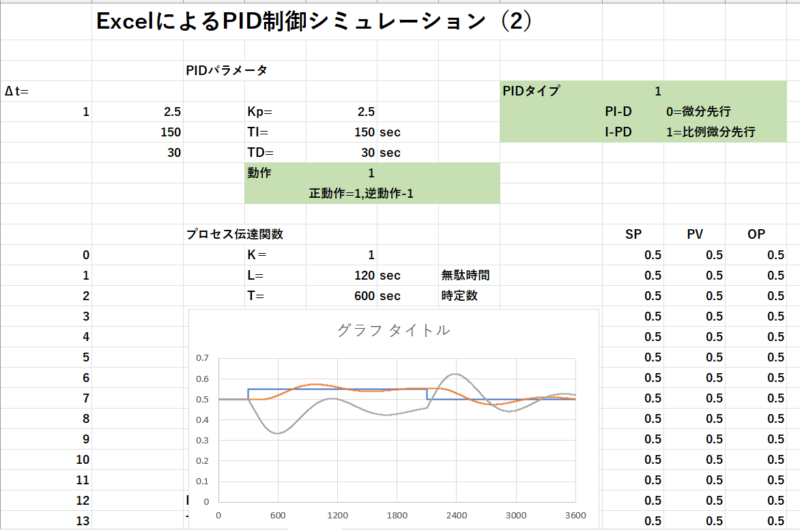
設定値は300秒から2100秒までが0.55でそれ以外は0.5です。
2-2.チューニング用シートの作成(1)
このExcelファイルに、新しいシートを追加しチューニング用のシートとし、下記を入力します。

- A列
時間を設定します。ここでは、1秒周期で3600秒までとします。 - E6 比例ゲイン(KP) = 2.5
- E7 積分時間(TI) = 150 秒
- E8 微分時間 =G8*E7 (微分時間は積分時間より計算します。微分時間≦0.2の制限を入れるため)
- E9 動作 -1(逆動作)
- G8 微分時間/積分時間(初期値0.2)
- D13 希望する整定時間 1200秒
- D14 参照モデルの無駄時間 初期値 60秒
- 整定時間、無駄時間から参照モデルの一次遅れの時定数を計算 =(D13-D14)/(4.4*3^0.6)
- I13~ 設定値変更データのSP =定位系!I13~
- J13~ 設定値変更データのPV =定位系!J13~
- K13~ 設定値変更データのOP =定位系!K13~
2-3.チューニング用シートの作成(2)
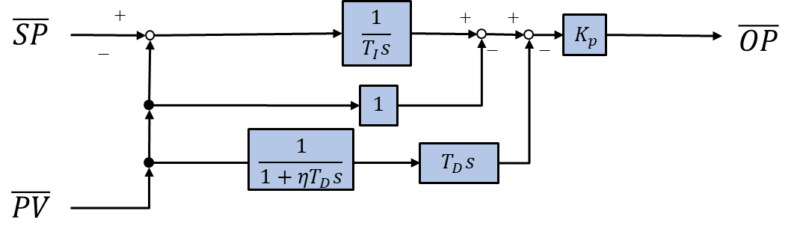
下記ブロック線図を参考に\(PV\),\(OP\)から\(\overline{SP}\)を計算します。
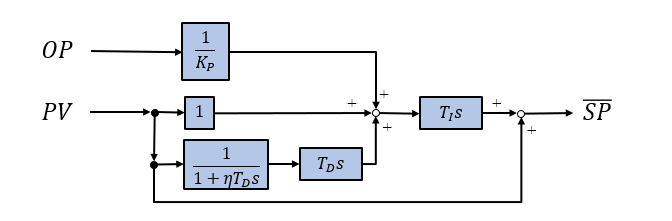
このExcelファイルに、新しいシートを追加しチューニング用のシートとし、上記ブロック線図を入力します。

- M,N列
比例の伝達関数を貼り付け
ゲイン(N9) =1/E6
入力 (M13~) =K14~ - O,P列
比例の伝達関数を貼り付け
ゲイン(P9) =1
入力 (O13~) =J13~ - Q,R列
1次遅れの伝達関数を貼り付け
時定数(R7) =E8*0.1+1E-30
入力 (Q13~) =J13~ - S,T列
微分の伝達関数を貼り付け
ゲイン(T11) =E8
入力 (S13~) =R13~ - U列
三つの信号の合計を計算
U13~ =N13-$E$9*P13-$E$9*T13~ - V,W列
微分の伝達関数を貼り付け
ゲイン(W11) =E7
入力 (V13~) =U13~です。 - U列
\(\overline{SP}\)の計算
X13~ =-$E$9*W13+J13~
以上で\(\overline{SP}\)の計算は終了です。
2-3.チューニング用シートの作成(3)
次に、参照モデルを使って\(\overline{SP}\)から\(\overline{PV}\)を計算します。
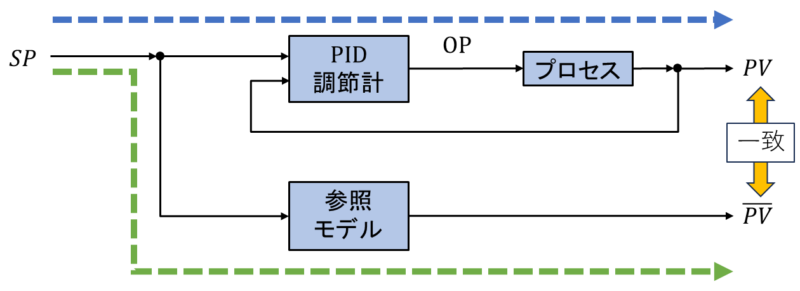
I-PD制御では、参照モデルは3次遅れ(n=3)になり、時定数は下式より計算します。
\(\tau=\frac{T_{99}}{4.4n^{0.6}}\)
チューニング用のシートに、参照モデルによる\(\overline{PV}\)の計算を追加します。
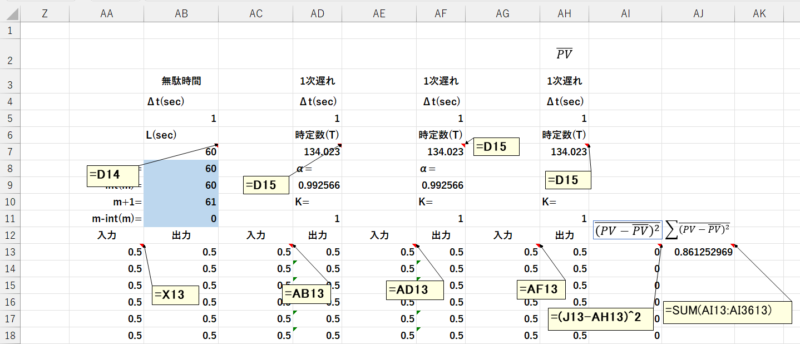
- AA,AB列
無駄時間の伝達関数を貼り付け
無駄時間(AB7) =D14
入力 (AA13~) =X13~ - AC,AD列
1次遅れの伝達関数を貼り付け
時定数(AD7) =D15
入力 (AC13~) =AB13~ - AE,AF列
1次遅れの伝達関数を貼り付け
時定数(AF7) =D15
入力 (AE13~) =AD13~ - AG,AH列
1次遅れの伝達関数を貼り付け
時定数(AH7) =D15
入力 (AG13~) =AF13~
以上で\(\overline{PV}\)の計算は終了です。
次に\(\Sigma(PV-\overline{PV})^2\)の計算になります。
- AI列
AI13~) =(J13-AH13)^2 - AJ13
=SUM(AI13:AI3613)
これで\(\Sigma(PV-\overline{PV})^2\)が計算できます。
これで、準備ができたので、チューニングを実行します。
3-1.ソルバーの設定
チューニングは、\(\Sigma(PV-\overline{PV})^2\)を最小とするP,I,Dパラメータ及び参照モデルの無駄時間を求めることになります。
ここではExcelのソルバーを使用します。
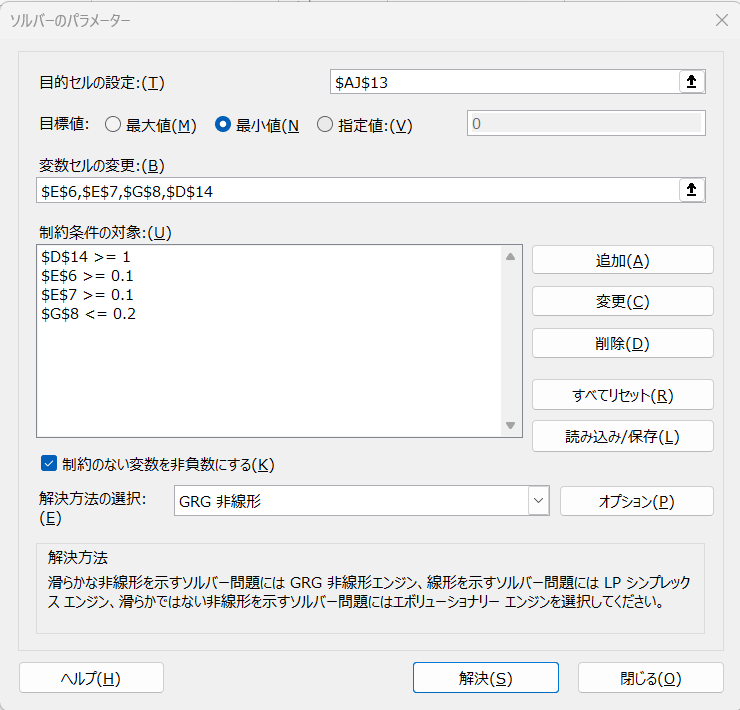
目的セルは$AJ$13で、\(\Sigma(PV-\overline{PV})^2\)で、目標値は最小です。
変数セルと制約条件は次の通りです。
- Kp E6、制約条件 0.1 以上
- TI E7、制約条件 0.1 以上
- TD/TI G8、制約条件 0.2以下
- 無駄時間 D14、1以上
その他は、デフォルトです。
3-2.チューニングの実行
ソルバーを実行します。
結果は次の通りです。
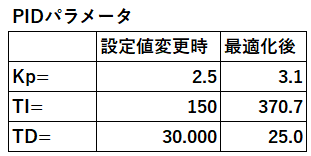
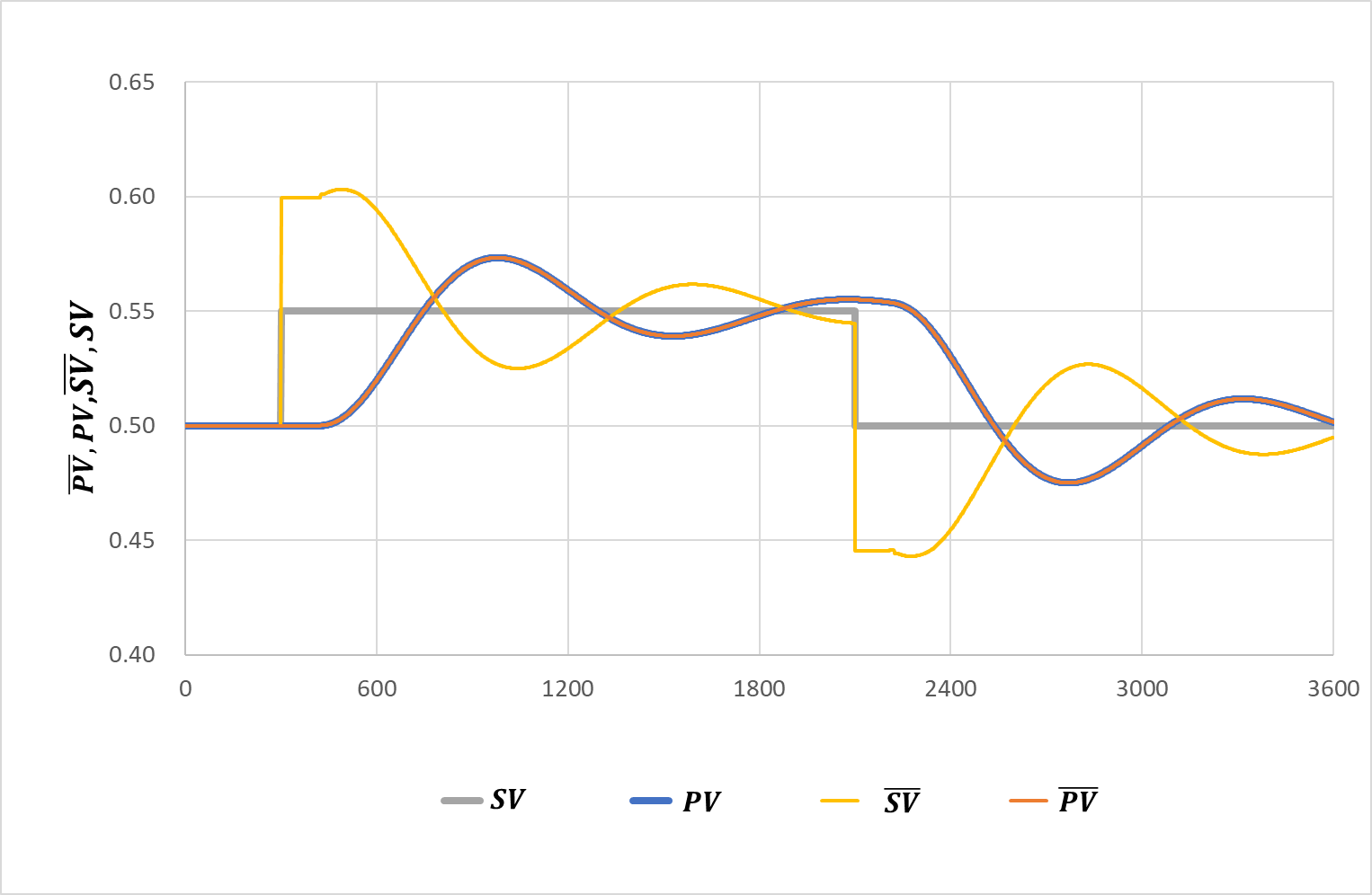
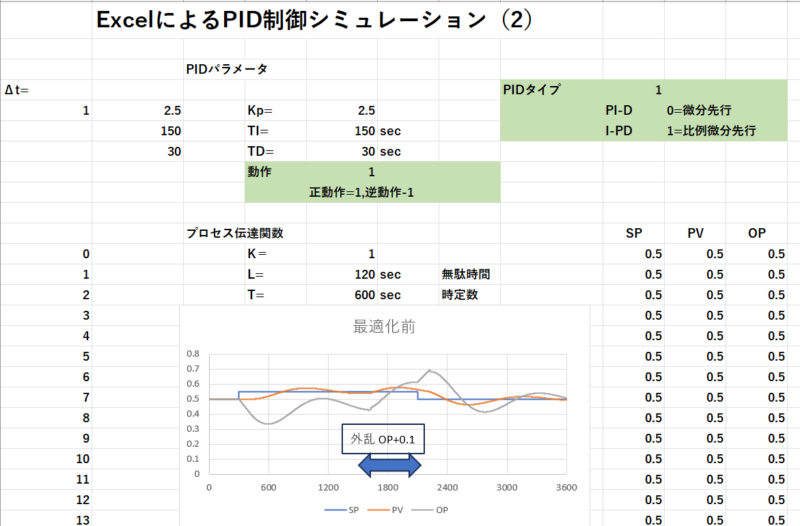
最適化前後で制御状態をシミュレーションすると下図のようになり、最適化がうまくいったことがわかります。
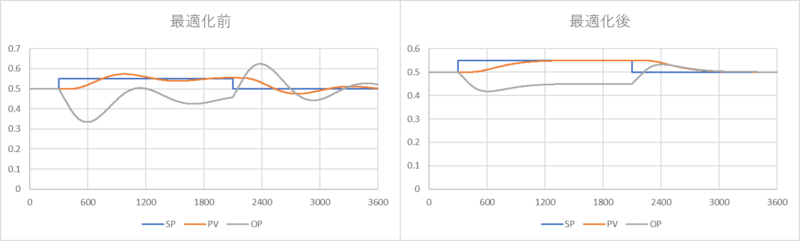
また、設定変更時の\(PV\),\(SP\)と最適化後の\(\overline{PV}\),\(\overline{SP}\)の関係は下記の通りです。
\(PV\)と\(\overline{PV}\)が一致するよう\(\overline{SP}\)がうまく調整していることがわかります。
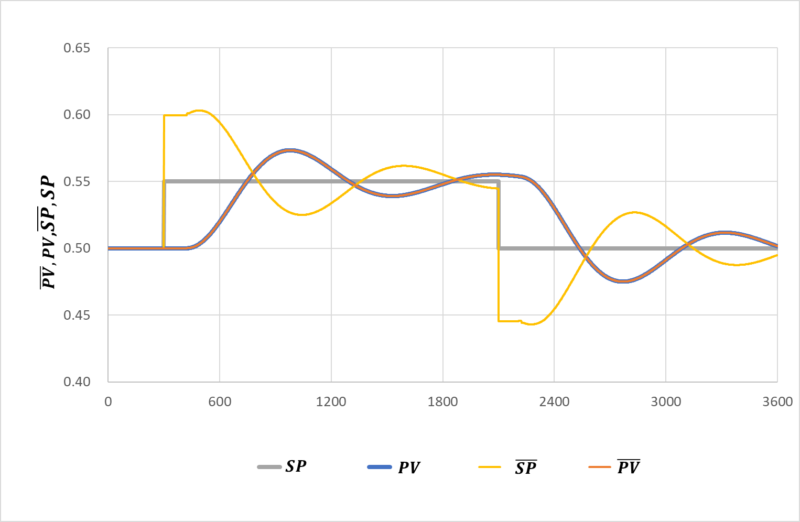
以上の例は、外乱のない状態のデータを使用しており、うまく最適化出来て当たり前と言うことも出来ます。
3-3.外乱ありの場合
そこで、外乱があるの場合についてチューニングを行いました。
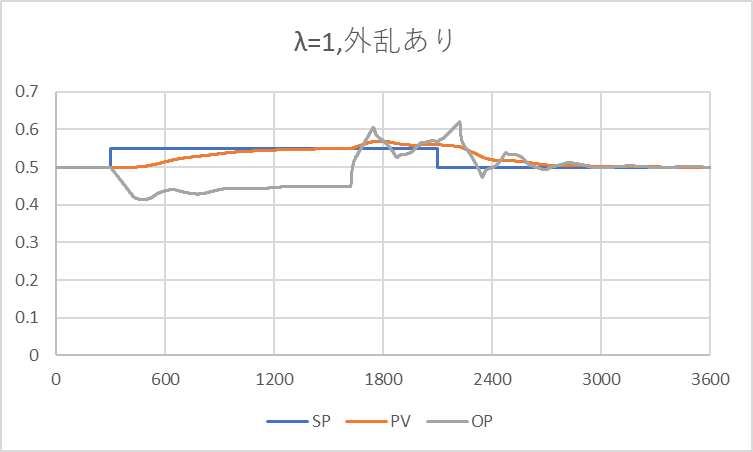
下図のように、1500~2100秒でOPに+0.1の外乱があった場合について、最適化しました。
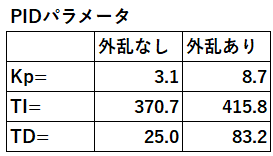
結果を、下表に示す。外乱なしに比べ、Kp,TI,TDとも大きな値となった。
このパラメータを使った場合の制御シミュレーションは、発散するという結果でした。
4.目的関数
今まで紹介した、PV値の参照モデルとの一致のみを評価してP,I,Dパラメータの最適化を行う方法では、対応不十分であり、下記資料のOP値も使った目的関数を取り入れることにしました。
小河 守正;化学工学,85,115-118 (2021)
4-1.目的関数
目的関数は次式により求めます。
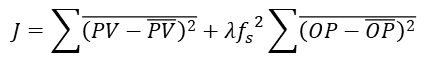

\(\overline{OP}\)は、P,IDパラメータと\(\overline{SP}\),\(\overline{PV}\)から計算します。
4-2.\(\overline{OP}\) の計算
はじめに\(\overline{OP}\)計算します。
この計算は、\(\overline{SP}\)、\(\overline{OP}\)及びP,I,Dパラメータから計算するので、”ExcelによるPID制御のシミュレーション(2)”のシートを使えば計算できます。
- 今まで作業していたシートの名前をSheetAにします。
- “ExcelによるPID制御のシミュレーション(2)”で作成したExcelシート(定位型)を使用し、設定値変更データを作成したシートをコピーしてSheetBとします。

SheetBの変更
- E6 =SheetA!E6, E7 =SheetA!E7, E8 =SheetA!E8, E9 =SheetA!E9, I5 =SheetA!I5 (SheetAの値を使用する。)
- I5 =SheetA!I5
- I13~ =SheetA!X13~ (SheetAの計算結果 \(\overline{SP}\))
- J13~ =SheetA!IAH13~ (SheetAの計算結果 \(\overline{PV}\))
- K13~ =SheetA!IK13~ (SheetAの設定値変更データ \(OP\))
- 赤色部分(C12:G15)を消去
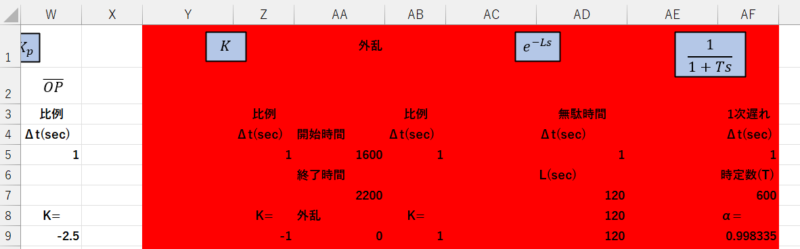
- W列に\(\overline{SP}\)が計算されている。
- 赤色部分(Y~AF列)の削除
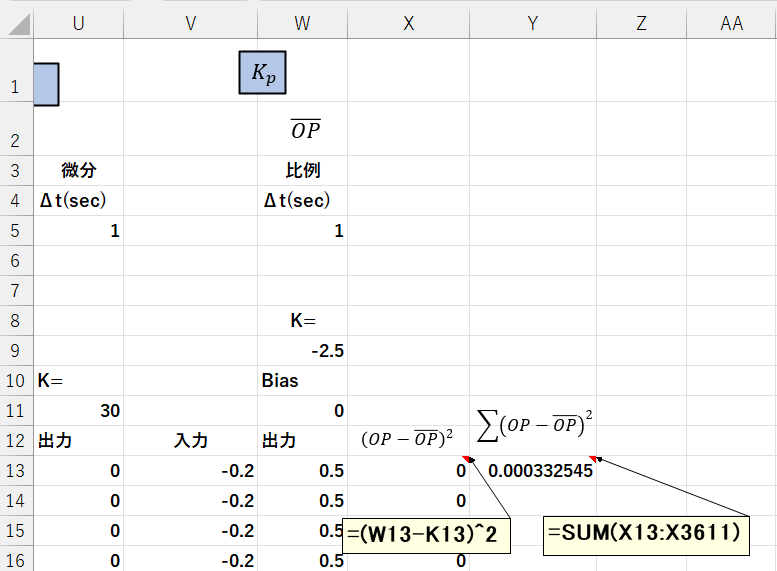
- X13~ =(W13-K13)^2 ~ ( \((PV-\overline{PV})^2\)の計算)
- Y13 =SUM(X13:X3611) (\(\Sigma(PV-\overline{PV})^2\)の計算)
4-3.目的関数の計算
SheetAでの作業になります。
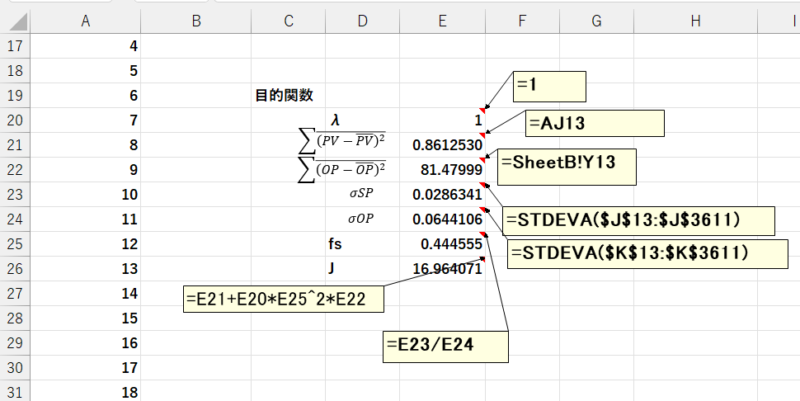
- E20 =1 ( λの値)
- E21 =AJ13 ( \((PV-\overline{PV})^2\)の計算)
- E22 =SheetB!Y13 ( \((OP-\overline{OP})^2\)の計算)
- E23 =STDEVA($J$13:$J$3611) (SVの標準偏差の計算)
- E24 =STDEVA($K$13:$K$3611) (OPの標準偏差の計算)
- E25 =E23/E24 (スケーリングファクターの計算)
- E26 ==E21+E20*E25^2*E22 (目的関数の計算)
4-4.最適化の実行
以上で最適化の準備が整いましたので、最適化を実行します。
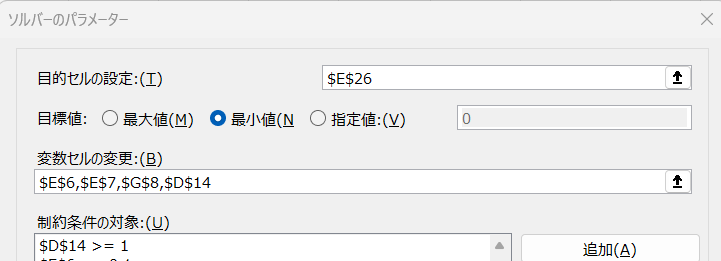
ソルバーの目的セルをAJ13からE26に変更します。
4-5.最適化の実行結果
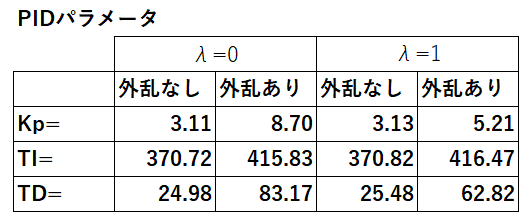
実行結果を下表に示します。
PV及びOPを使った目的関数を使用した時(λ=1)、外乱ありの場合Kpの増加が押さえられていることが分かります。
5.次回の予定
実次回は、微分先行型PID制御(PI-D制御)の場合について紹介する予定です。