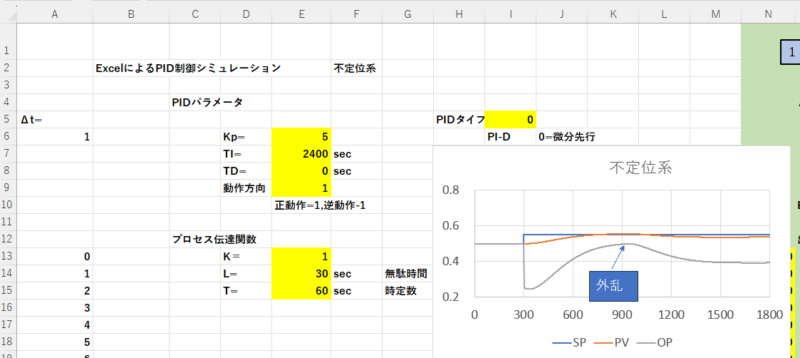
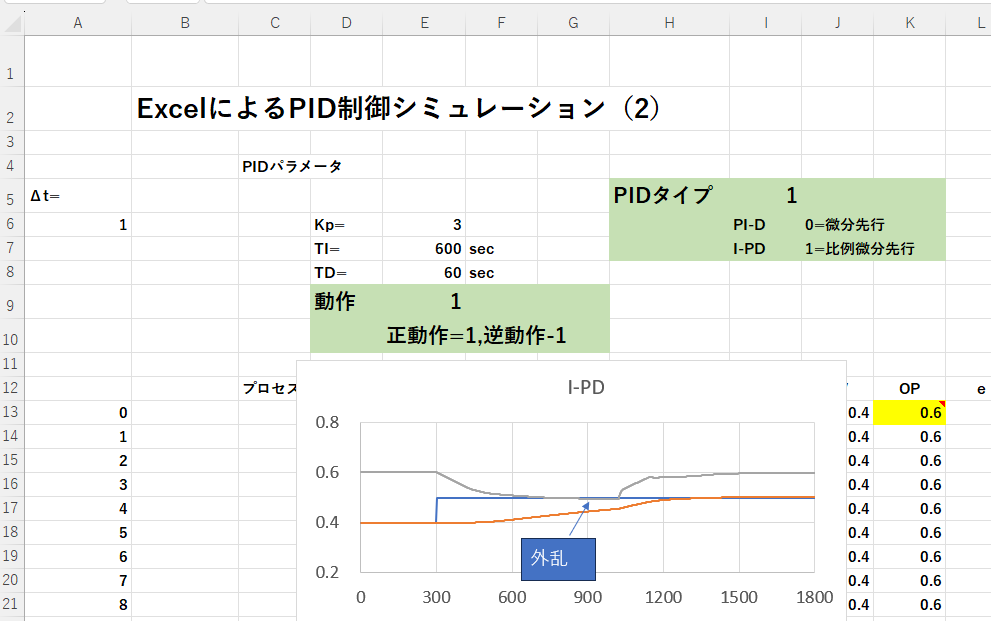
先に紹介した”ExcelによるPID制御のシミュレーション”は、微分先行型PID制御、逆動作、定位系でのシミュレーションでした。
ここでは、次の機能を持つようExcelを変更する方法を紹介します。
- 制御方法 微分先行PID制御(PI-D制御)、比例微分先行PID制御(I-PD制御)
- シミュレーション方法 設定値変更、外乱
- 動作方向 正動作、逆動作
- プロセス 定位系、不定位系(積分系)
1-1.正動作と逆動作
正動作、逆動作とは、PID制御の偏差(\(e\))と出力(\(OP\))の関係を言います。
偏差(\(e\))が増加したとき、出力(\(OP\))も増加するときを正動作(同じ向き)と言い、減少する時を逆動作(逆の向き)と言います。
一般的な流量制御が逆動作で、抜出し量で制御するレベル制御が正動作となります。
偏差(\(e\))の式で考えると次のようになります。
- 逆動作 \(e = SP – PV\)
- 正動作 \(e = PV – SP\)
1-2.正動作と逆動作の違い(PID制御)
逆動作と正動作をブロック線図で比較してみます。
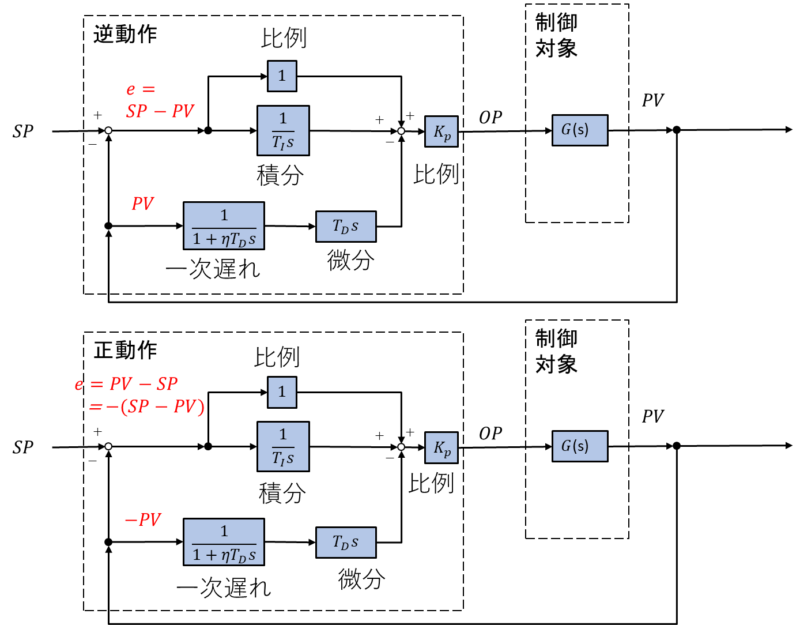
上図のように、正動作では比例、積分の入力\(e\)及び不完全微分(一次遅れ+微分)の入力\(PV\)の符号がプラスからマイナスに変化します。
これはブロック線図の等価変換を使うと、\(K_P\)の符号をマイナスにしたことと同になります。
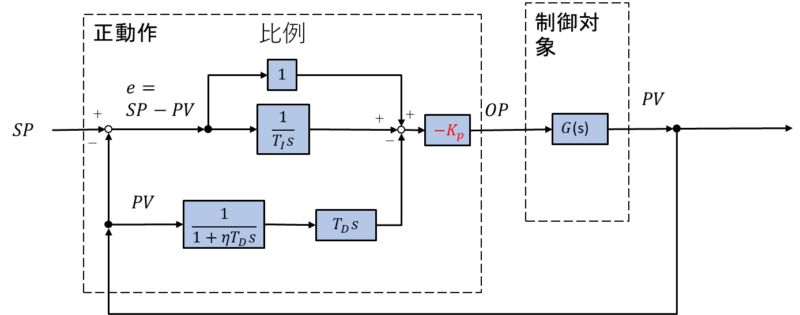
1-2.正動作と逆動作の違い(制御対象)
逆動作と正動作では制御対象の挙動も変わります。
ここでは線形を想定しているので、\(K=1\)の時\(OP\)と\(PV\)の関係は下図のようになります。
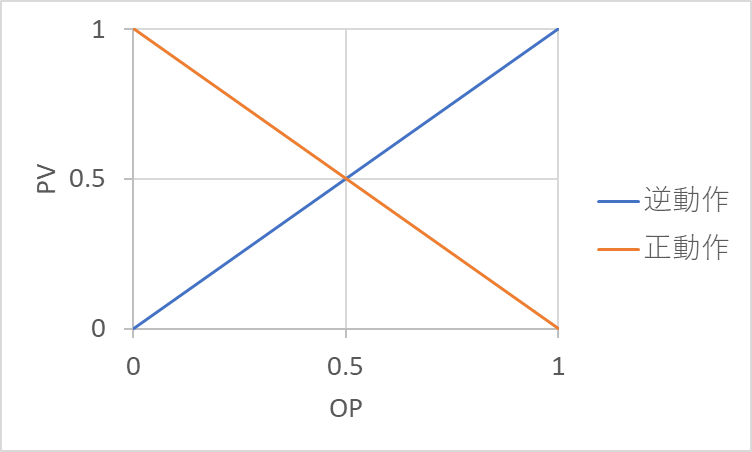
それぞれ下式で表現します
- 逆動作
- \(PV = 1.0 OP + 0.0\)
- 正動作
- \(PV = -1.0 OP +1.0\)
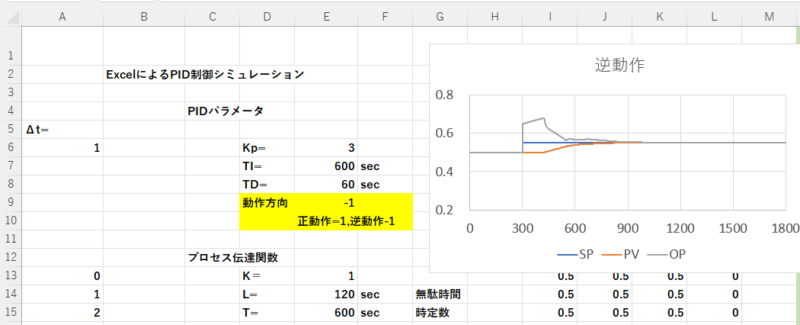
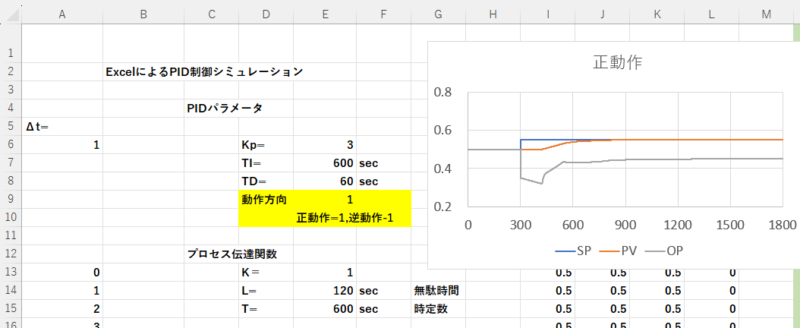
1-3.Excelでの正動作と逆動作の設定
逆動作と正動作の設定をExcelで行う場合について説明します。
先に紹介した”ExcelによるPID制御のシミュレーション”のワークシートを使います。
Step1
セルE9に正動作であれば1を、逆動作であれば-1を入れます。
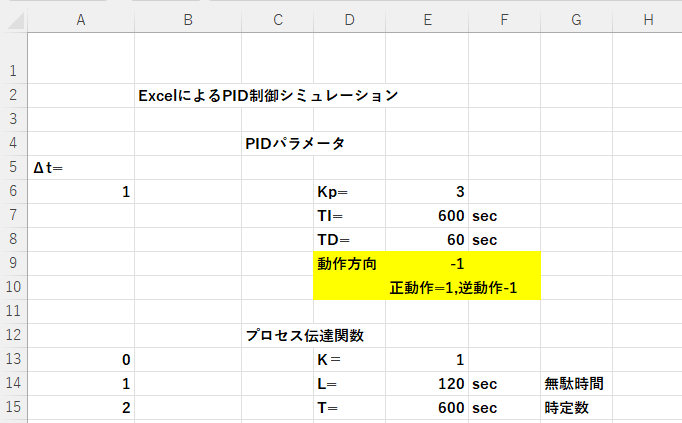
Step2
\(K_P\)のゲイン(K=)に式=E6*-E9を入力する。(E9が1の時符号をプラスからマイナスにする。)
\(K\)のゲイン(K=)に式=IF(E9=-1,1,IF(E9=1,-1))を入力する。(E9が1の時 -1,E9が-1の時 1にする。)
\(K\)のBiasに式=IF(E9=-1,0,IF(E9=1,1))を入力する。(E9が1の時 1,E9が-1の時 0にする。)
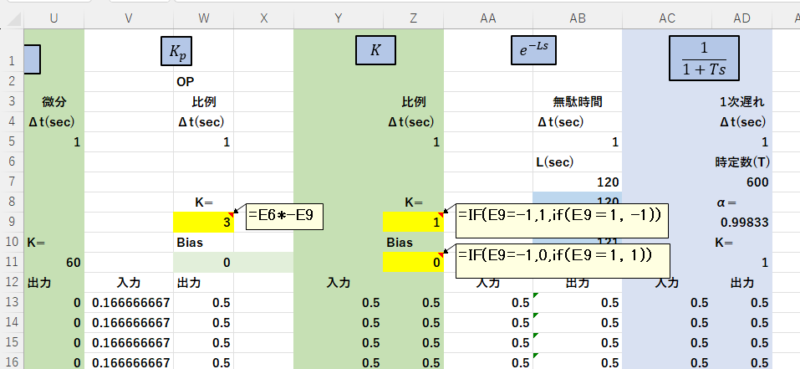
Step3
OPの初期値(セルK13)に式=(J13-Z11)/Z9を入力する。(正動作、逆動作でOPとPVの関係が変わるため。)
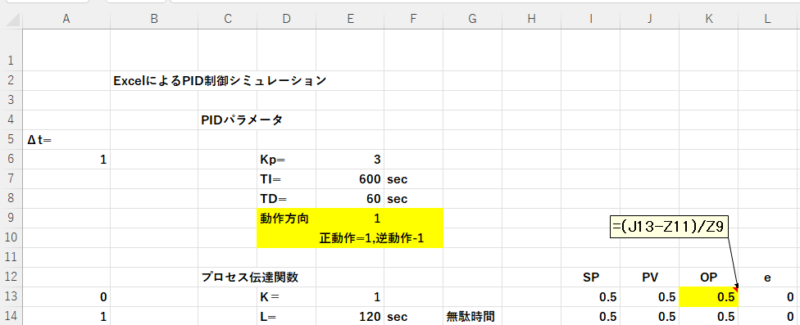
以上の変更で、正動作、逆動作に対応できるようになります。
2-1.外乱の取り込み
PID制御のシミュレーションでは、設定値変更時とともに外乱発生時の挙動も重要です。
ここで更に外乱の機能も追加します。
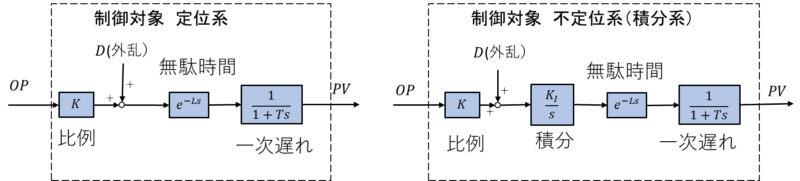
外乱の表し方にはいろいろありますが、ここでは下記のブロック線図のようにします。(PI-D制御、逆動作)
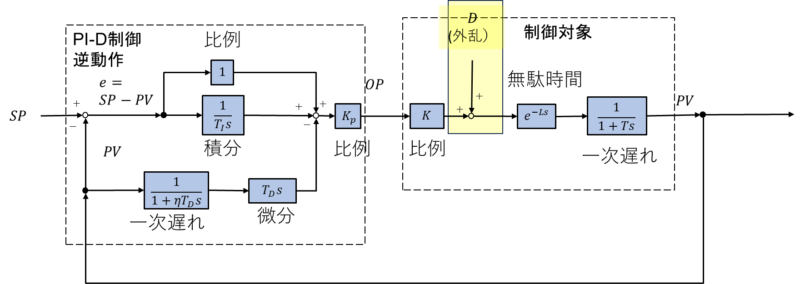
2-2.Excelでの外乱の設定
先ほどのExcelシートに外乱を新たに加えます。
Step1
無駄時間\(e^{-Ls}\)の前に新たに外乱として比例の伝達関数を挿入します。
Step2
K=1、Bias=0とし、入力には900秒後に外乱0.1を発生させるという意味で、=IF(A13>=900,0.1,0)を入力します。
Step3
無駄時間\(e^{-Ls}\)の入力は、=Z13+AB13となります。
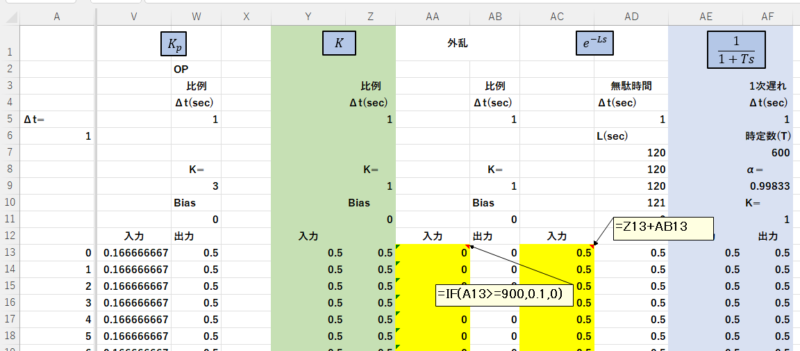
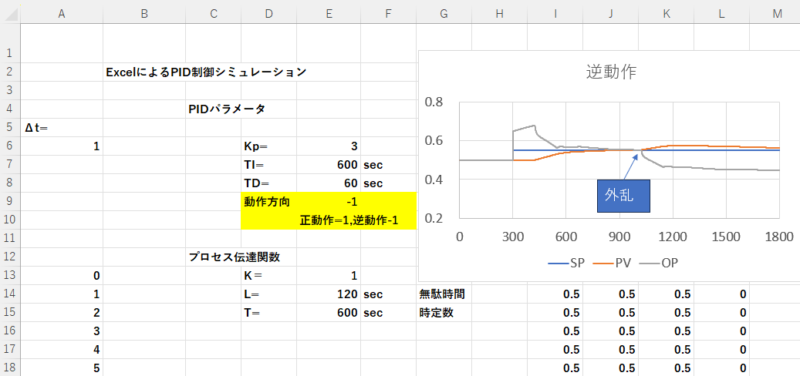
以上により下図のように外乱のシミュレーションが可能になります。
ここでは、設定値変更より整定時間が長くかかっていることがわかります。
3-1.PI-D、I-PD制御
PID制御にはいろいろなタイプがあり、その代表的なものが微分先行PID制御(PI-D制御)と比例微分先行PID制御(I-PD制御)です。
ブロック線図にすると下図のようになります。(逆動作)
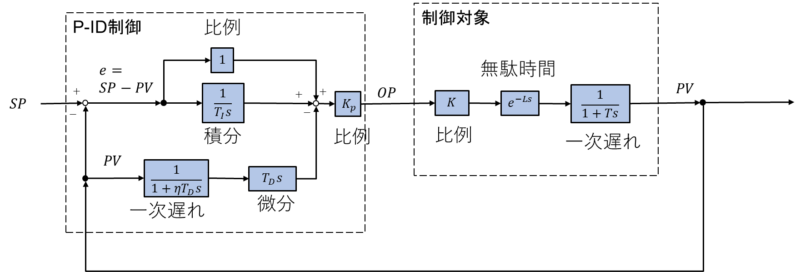
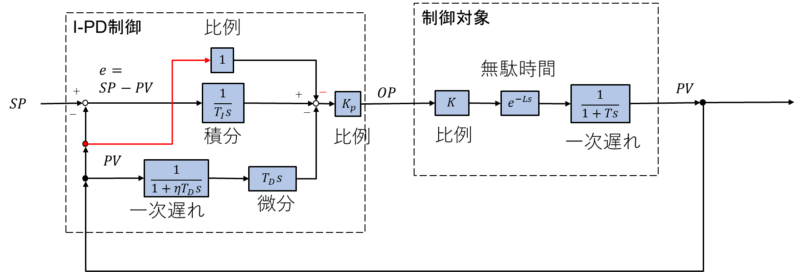
I-PD制御では、比例の入力が\(e\)から\(PV\)に変わり、\(K_P\)の入力も比例の出力がマイナスに変更されます。
3-2.ExcelでのPI-D、I-PD制御の設定
先ほどのExcelシートにPI-D,I-PD制御を加えます。
Step1
セルI5に、PI-Dの時は0を、I-PDの時は1を入れます。
Step2
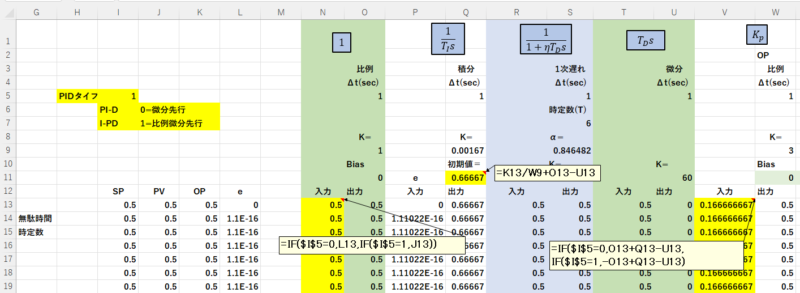
比例の入力を=IF($I$5=0,L13,IF($I$5=1,J13))とします。(PI-Dでは\(e\),I-PDでは\(PV\) )
Step3
積分の初期値を=K13/W9+O13-U13とします。(時間0での\(OP\)が0.5)
Step4
\(K_P\)の入力を=IF($I$5=0,O13+Q13-U13,IF($I$5=1,-O13+Q13-U13))とします。(I-PDの時は-比例)
以上でPI-D制御とI-PD制御の切り替えができました。
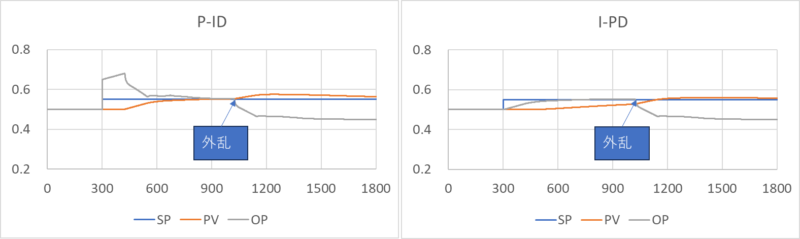
同じPIDパラメータでは、設定値変更時の挙動が大きく違うことがわかります。
4-1.定位系、不定位系
今までの例では、制御対象(プロセス)を流量制御に代表される無駄時間+一次遅れ系としました。これを定位系と呼びます。
一方、制御対象にはレベル制御のような積分系を含むものもあり、これを不定位系(積分系)と呼びます。
そこで、Excelにこの機能も追加します。
ただし、定位系-不定位系の切換えが煩雑になるので、これまでのExcelプログラムを定位系の名前を入れて保存し、新たにプロセスの部分を変更し不定位系のプログラムとします。
4-2.Excelでの不定位系の設定
Step1
抜出によるレベル制御を想定し正動作、PIDタイプはPI-Dとしておきます。
また、制御状態も変わるため、PIDパラメータ及びプロセスの伝達関数も変更しておきます。

Step2
ブロック線図に従って、無駄時間\(e^{-Ls}\)の前に積分の伝達関数を挿入します。
外乱は、抜出によるレベル制御の場合は、流入量に相当します。はじめは流入=抜出(流出)とし、900秒後に0.1増加する設定とし式=IF(A13>=900,$Z$13+0.1,$Z$13)を入力します。
積分の係数Kは=1/1200を入力します。これは、OP100%で抜出した場合、流入が0の時満液状態から1200秒後に空になることを意味します。
初期値はPVの初期値で、式=J13を入力します。
積分の入力は流入と流出の差で、式=Z13-AB13を入力します。
無駄時間の入力は積分の出力であり、式=AD13を入力します。
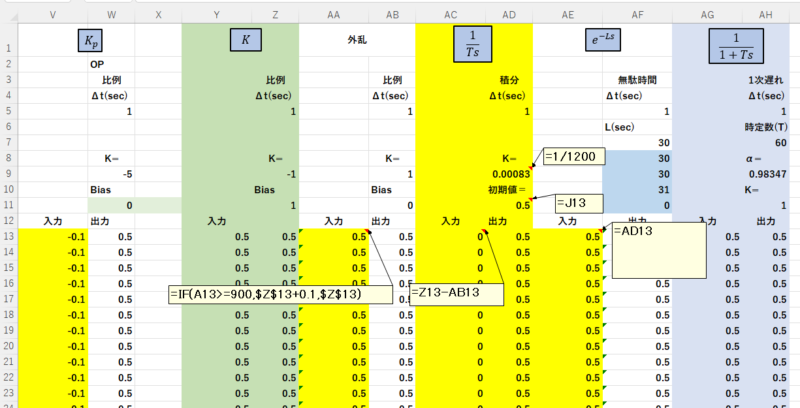
以上の変更で、不定位系のPID制御のシミュレーションができるようになりました。