CSTR(連続槽型反応器)の設計は、単一反応で一次反応の場合は、代数方程式となり、容易に解くことが出来ます。
しかしながら、複合反応の場合は、連立非線形代数方程式となり、解くのが難しくなります。
そこで、蒸留計算で使用したリラキゼーション法を使用します。すなわち、非定常状態の物質収支式(微分方程式)を数値積分し、定常状態となった時点を解とする方法を用いて、Excelを使用して計算する例を紹介します。ここでもExcelの反復計算機能を利用します。
目次
1.CSTR(連続槽型反応器)の例
下記の仮定のもと計算を行います。
- 液相反応とし反応に伴う密度変化がない。
操作条件
- 量論式、反応速度式
- \(\text{A + B} \rightarrow \text{C} \quad r_1 = k_1 C_A C_B\quad k_1=1.0\)
- \(\text{C} \rightarrow \text{D} \quad r_2 = k_2 C_C\quad k_2=3.0\)
- \(\text{A +C} \rightarrow \text{E} \quad r_3 = k_3 C_A C_C\quad k_1=0.5\)
- 単位 \(r_n : kmol / m^3 ・ hr , C_i : kmol / m^3 \)
- 反応原料
- 体積流量 \(1.0 \, \text{m}^3/\text{hr}\)
- 濃度 \(C_{A0} = 6.0 , C_{B0}=5.0 , C_{C0} = 0.0 , C_{D0}=0.0 , C_{E0} = 0.0\)
- 反応器体積 \(1.0 \, \text{m}^3\)
2.物質収支式
各成分の物質収支式は非定常状態とすると次の様になります。
- \(\frac{dn_A}{dt} = vC_{A0} + r_1 V + r_2 V + r_3 V – vC_A = vC_{A0} + k_1 C_A C_B V + k_2 C_C V + k_3 C_A C_C V – vC_A \)
- \(\frac{dn_B}{dt} = vC_{B0} + r_1 V + r_2 V + r_3 V – vC_B = vC_{B0} + k_1 C_A C_B V + k_2 C_C V + k_3 C_A C_C V – vC_B \)
- \(\frac{dn_C}{dt} = vC_{C0} + r_1 V + r_2 V + r_3 V – vC_C = vC_{C0} + k_1 C_A C_B V + k_2 C_C V + k_3 C_A C_C V – vC_C \)
- \(\frac{dn_D}{dt} = vC_{D0} + r_1 V + r_2 V + r_3 V – vC_D = vC_{D0} + k_1 C_A C_B V + k_2 C_C V + k_3 C_A C_C V – vC_D \)
- \(\frac{dn_E}{dt} = vC_{E0} + r_1 V + r_2 V + r_3 V – vC_E = vC_{E0} + k_1 C_A C_B V + k_2 C_C V + k_3 C_A C_C V – vC_E \)
この微分方程式をオイラー法で数値積分することにより、定常解を得ることが出来ます。
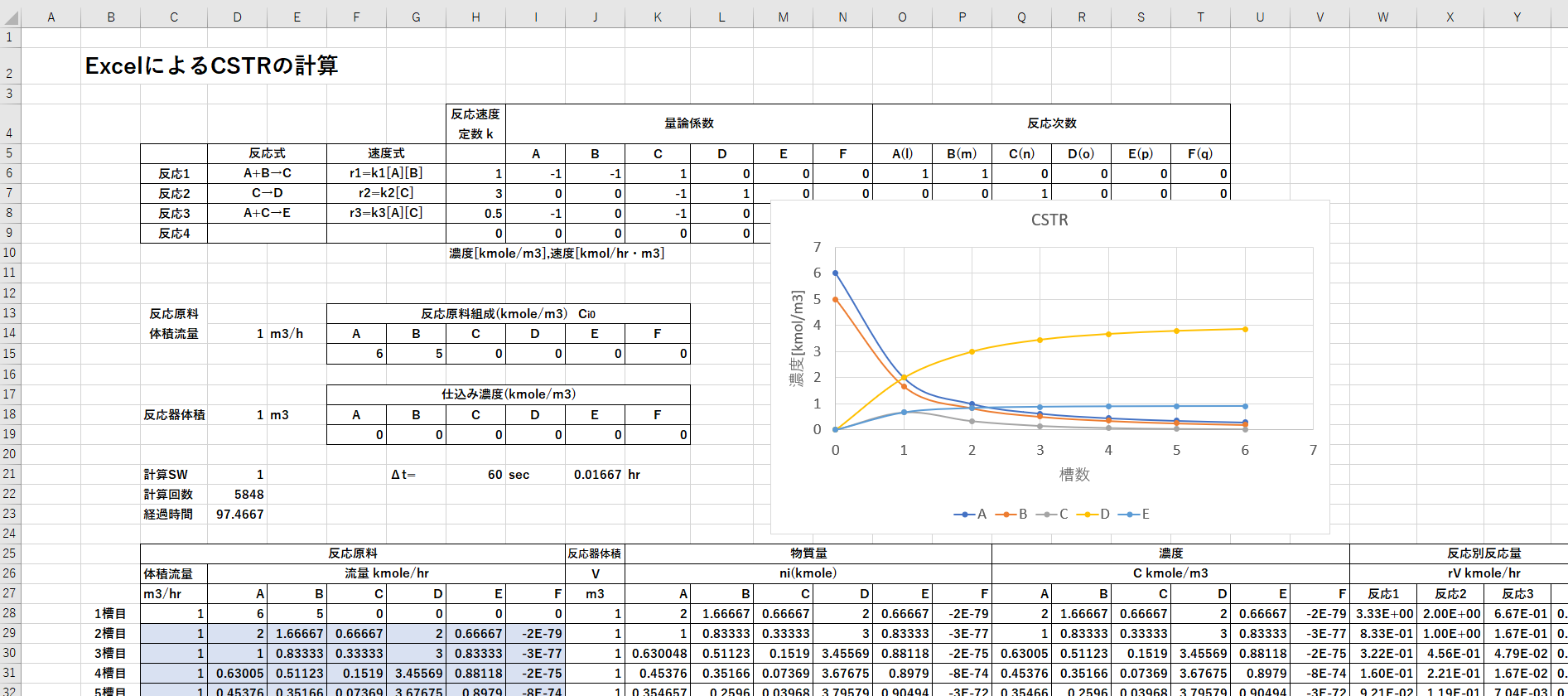
3. ExcelによるCSTRの計算
この例では、反応が違っても対応できるよう次のようにしています。
- 複数の反応(最大4)に対応できる、
- 最大6成分に対応できる。
- 物質収支の計算式の変更を不要とするため、反応の量論係数、反応次数、反応速度定数を入力する方法とする。
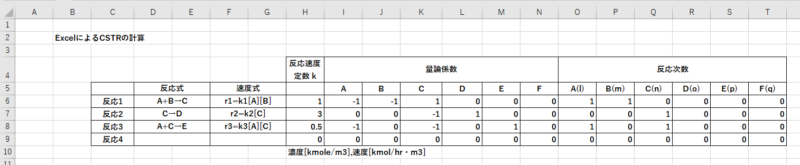
3-1. 反応の定義
反応1~4に、下記項目を入力します。
- 反応式、速度式を入れます。これは、分かりやすくするためで特に計算には関係しません。
- 反応速度定数を入力します。(H6~H9)
- 量論係数を入力します。原料側はマイナスとなります。(I6~N9)
- 反応次数を入力します。(O6~T9)
3-2. 原料供給、反応器体積
反応原料及び反応器体積に、下記項目を入力します。
- 反応原料体積流量を入力します。(D14)
- 反応原料組成を入力します。(F15~K15)
- 反応器体積を入力します。(D18)
- 仕込み濃度(初期濃度)を入力します。(F19~K19)
- 初期濃度は0でかまいません。

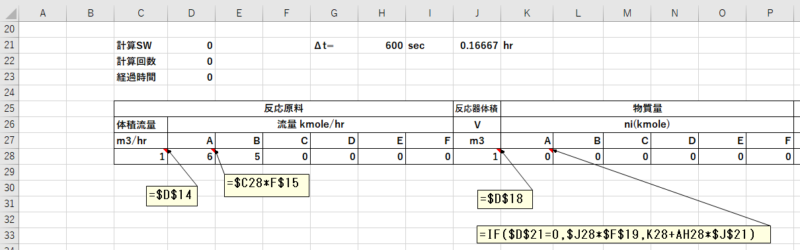
3-3. 反復計算、数値積分の設定
- ここでも反復計算を使うので、計算SWを入力します。(D21)
- 計算回数、経過時間も計算させます。(D22,D23)
- 数値積分の刻み幅(Δt)を入力します。(H21)

3-4. 反応計算(1)
- 反応原料の体積流量の式を入力します。(C28)
- 反応原料の流量の式を入力します。(D28,I28)
- 反応器体積の式を入力します。(J28)
- 反応器内の物質量の式を入力します。(K28)
- 計算SW($D$21)が0の時は、反応器体積(\J28)×仕込濃度($F$19)となります。
- 計算SW($D$21)が0以外の時は、現在の値(K28)に\(\frac{dn_A}{dt}\) (AH28)×Δt($J$21)を加えた値となります。
3-4. 反応計算(2)
- 濃度の式を入力します。(Q28)
- 濃度は、次の反応量計算でべき乗されるため、0ではエラーとなります。
- このため、物質量(K28)が0の時は、0でない小さな数値(1e-20)としています。
- 反応別反応量の式を入力します。(W28)
- \(r_1 V = k_1 C_A^l C_B^m C_C^n C_D^o C_E^p C_F^q V\)

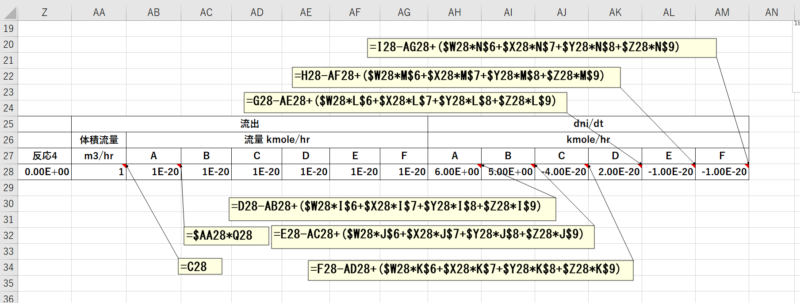
3-4. 反応計算(3)
- 流出の体積流量の式を入力します。(AA28)
- 流出の流量の式を入力します。(AB28,AG28)
- \(\frac{dn_A}{dt}\) の式を入力します。(AH28)
- \(\frac{dn_A}{dt} = v C_{A0} – v C_A+r_1 a_1 + r_2 a_2 + r_3 a_3 + r_4 a_4\)
- \(a_1\)~\(a_4\)は、反応1~4の量論係数を表します。
3-5. 反復計算の設定
この計算でも反復計算を使用します。
ファイル → オプション → 数式 で、下記画面を出します。
最大反復回数を100として、反復計算を行うにチェック入れてOKを押せば、反復計算を行います。
この例では、100回程度で定常解に収束します。
滞留時間( \(\frac{V}{v}\) )、刻み幅(Δt)で収束回数も変ります。また、ファンクションキーF9を押せば反復計算は再開されます。
以上で、CSTRの計算が出来るようになりました。


3-6. CSTRを直列に結合した場合の計算
CSTRは複数直列に結合し、反応率を上げるため直列に結合される場合があります。
このExcelシートでは、次の様に簡単に直列結合に対応できます。
- 28行をコピーして29行目に貼付けます。
- 2槽目(29行)の反応原料(C29~I29)を1槽目の流出(AB28~AG28)とします。
- 3槽目以降を追加する場合は、29行をコピーします。
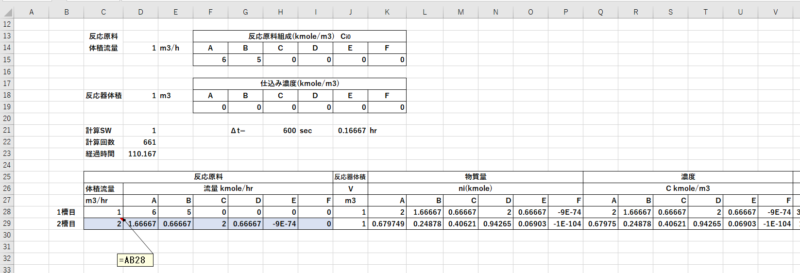
これを行うことにより、必要な槽を追加することが出来ます。