ExcelによるPID制御のチューニング(1)CHR法(1)では、PIDのチューニングの代表的な方法CHR法による、設定値変更時のチューニングについて、先に紹介した”ExcelによるPID制御のシミュレーション”を使った制御性の確認について紹介しました。
ここではCHR法の外乱に対する制御性の確認を、先に紹介した”ExcelによるPID制御のシミュレーション”を使った制御性の確認について紹介します。
1.CHR法
CHR法は、代表的なPIDパラメータの調整法で、制御対象のプロセスの動特性\(P(s)\)を無駄時間+一次遅れモデルとし、ゲイン\(K\)、一次遅れの時定数\(T\)、無駄時間\(L\)からPIDパラメータを求める方法です。
\(P(s) = \)\(\frac{K}{1 + Ts}\) \(e^{-Ls}\)
計算式は下表のようになっています。
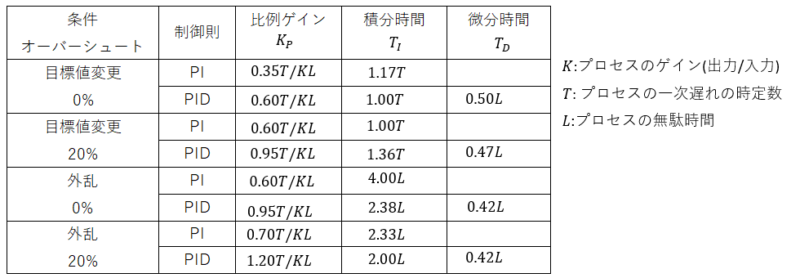
表からわかるように、条件として目標値変更と外乱があり、更にはオーバーシュート0%、20%に分かれています。
今回は、外乱について紹介します。
2.目標値変更、オーバーシュート0%、PID制御でのシミュレーション
初めに、外乱、オーバーシュート0%、PI-D制御でのシミュレーションを紹介します。
設定値変更では、CHR法が発表された年代(1952年)からPID制御としました。外乱時の対応についてもPID制御とします。
尚、外乱時はPID制御と微分先行PID制御(PI-D制御)と比例微分先行PID制御(I-PD制御)で制御状態に差はありません。
2-1.PID制御の変更[CHR法(1)に同じ]
先の”ExcelによるPID制御のシミュレーションでは、微分先行PID制御(PI-D制御)としてましたが、CHR法の発表の年代(1952年)から、下記のPID制御としました。
尚、外乱時はPID制御と微分先行PID制御(PI-D制御)と比例微分先行PID制御(I-PD制御)で制御状態に差はありません。
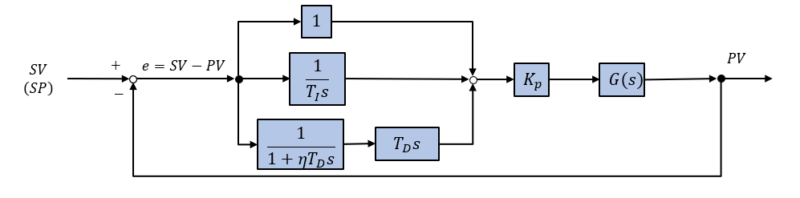
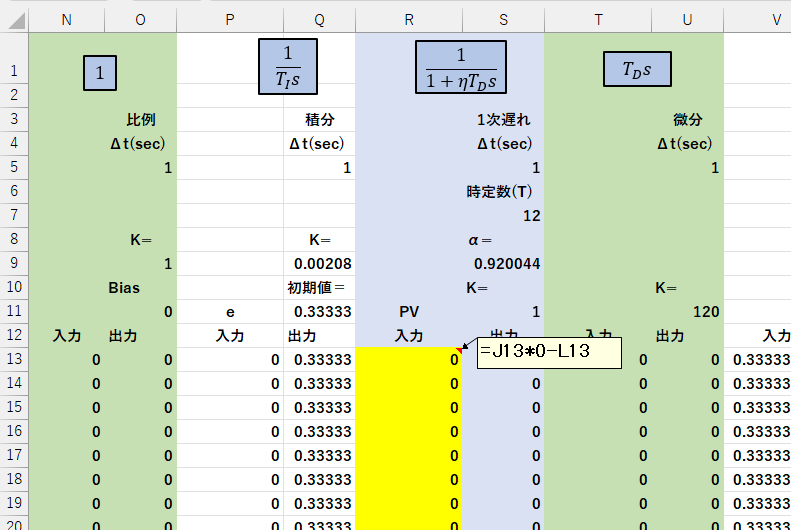
Excelでの変更点は、\(\frac{1}{1+\eta T_D s}\)の入力を\(PV\)から\(-e\)に変更することです。
2-2.外乱の表現
外乱の表し方にはいろいろありますが、ここでは下記のブロック線図のようにします。(PI-D制御、逆動作の例)
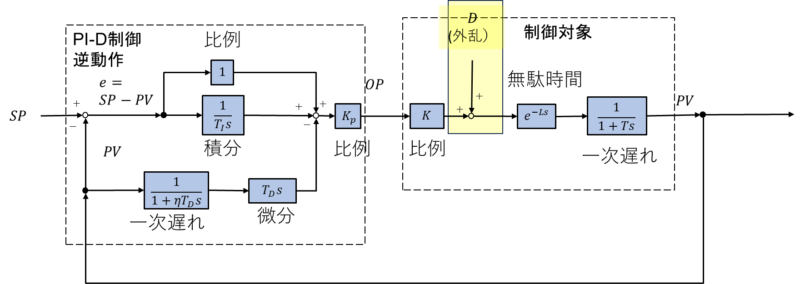
2-3.プロセスの動特性[CHR法(1)に同じ]
プロセスの動特性は、無駄時間+一次遅れ系です。
一次遅れの時定数\(T\)、無駄時間\(L\)の組み合わせは無数にあり、これらすべてで制御性を確認することは不可能です。
そこでプロセスの動特性の相似性に着目します。
\(\frac{L}{T}\)=一定とし、いくつかの時定数\(T\)でシミュレーションを行います。
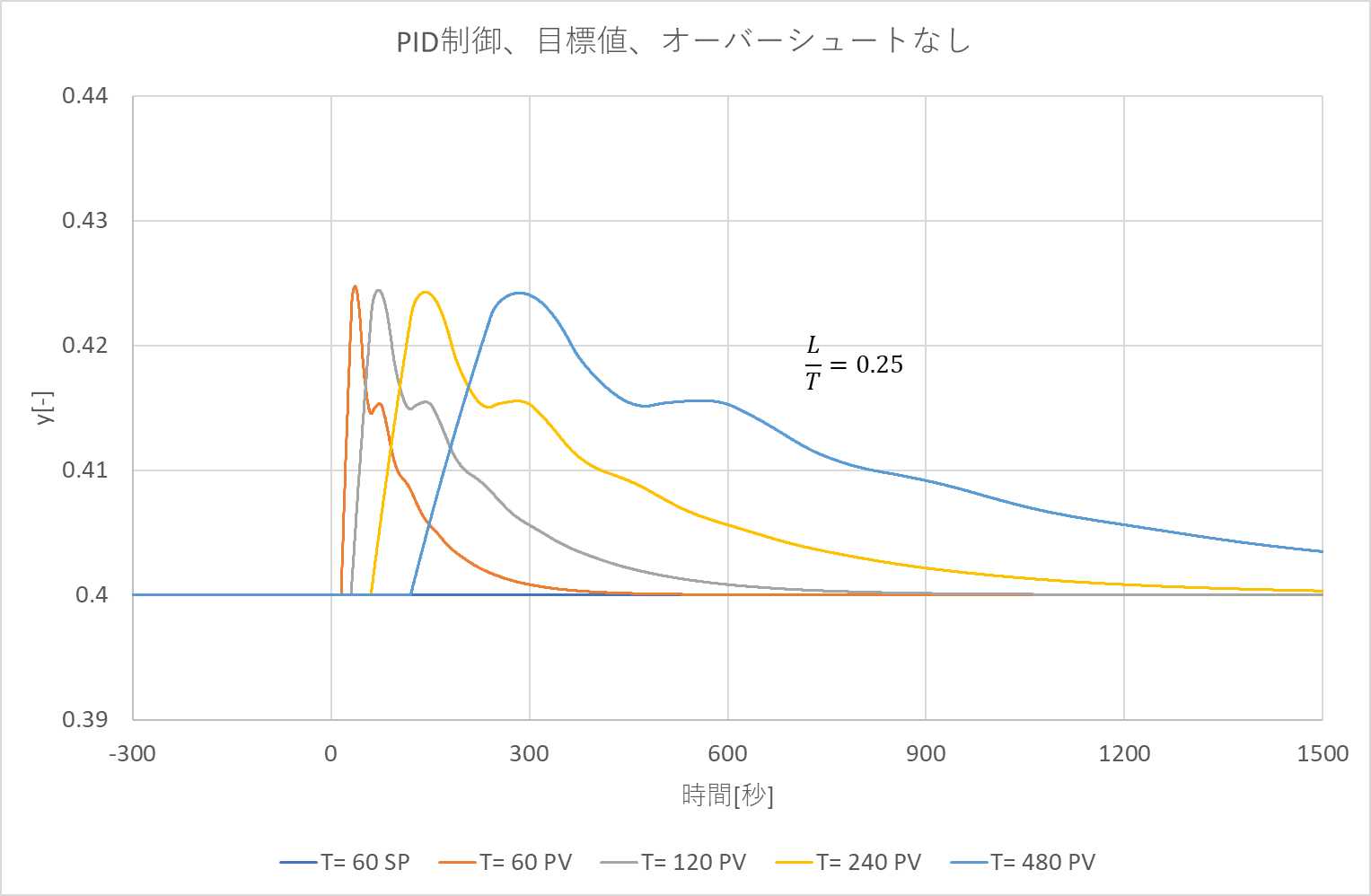
これは、\(\frac{L}{T}\)\(=0.25\)、\(T=60,120,240,480\)とした時のシミュレーションです。(\(K=1\))
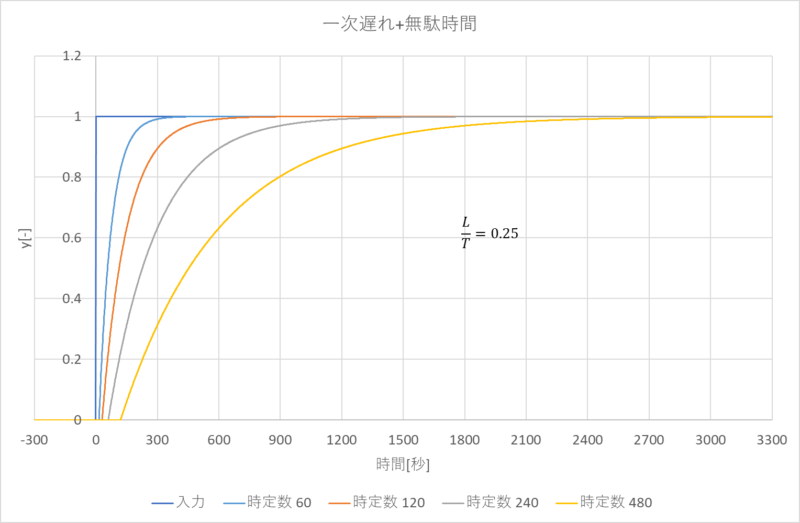
次に一次遅れの微分方程式の解析解\(y(t) = K(1 – e^{-\frac{t}{T}})\) に着目し、横軸を\(t\)から\(\frac{t}{T}\)に変更します。
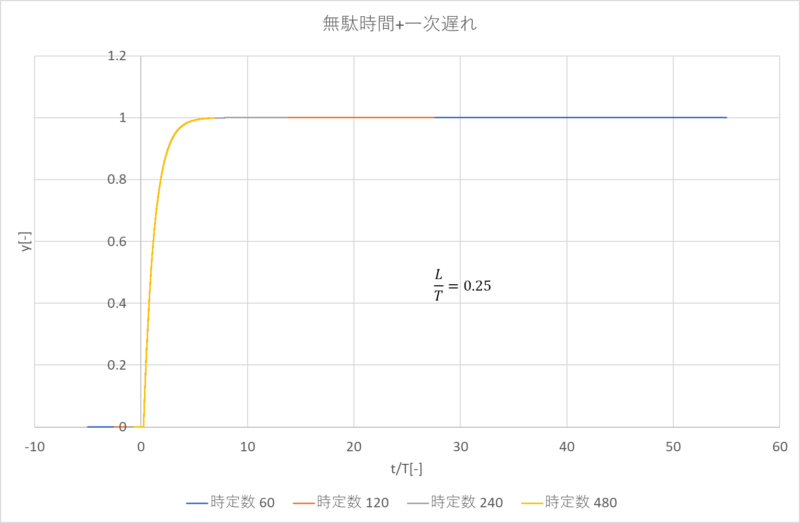
こうすることにより、時定数が違っても\(\frac{L}{T}\)が同じであれば、同一の曲線とすることができます。
つまり\(\frac{L}{T}\)が同じであれば、一つの時定数のグラフから他の時定数のグラフが推定可能になるわけです。
制御性の確認においても、このことが期待されます。
2-4.外乱、オーバーシュート0%、PID制御
外乱、オーバーシュート0%、PID制御でのシミュレーションを使い、制御性の確認を行います。
対象プロセスは、\(\frac{L}{T}\)\(=0.25\)、\(T=60,120,240,480\)です。(\(K=1\))
これが外乱時のPID制御の制御状態です。オーバーシュートもなく安定していることがわかります。
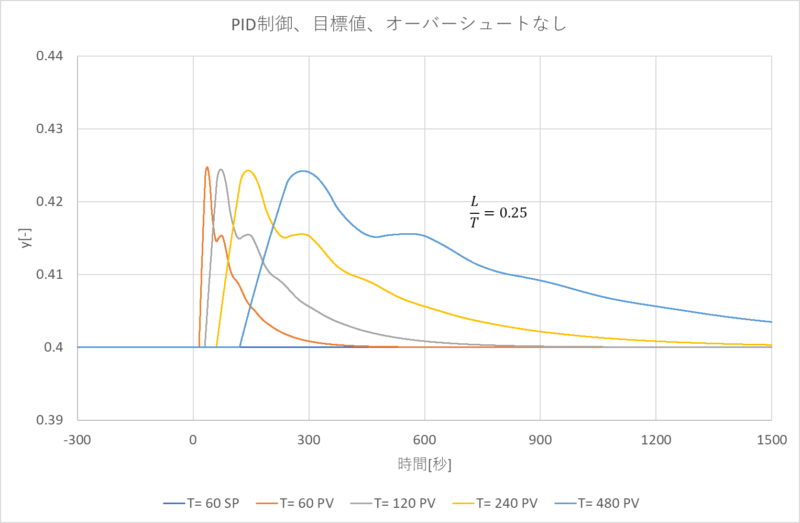
横軸を時間\(t\)から\(\frac{t}{T}\)に変えたのが次のグラフです。
予想通り各データが重なっていることがわかります。
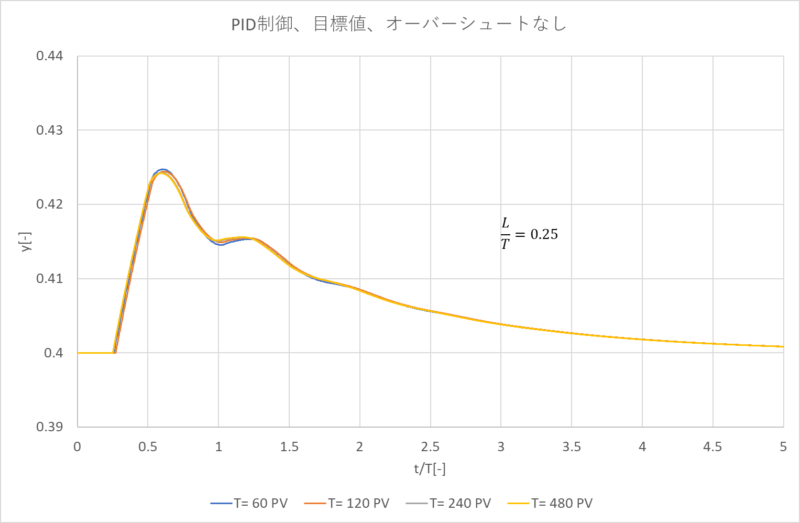
更に、\(\frac{L}{T}\)を\(0.50,0.75,1.00\)とした場合も下記グラフのように同様に重なります。
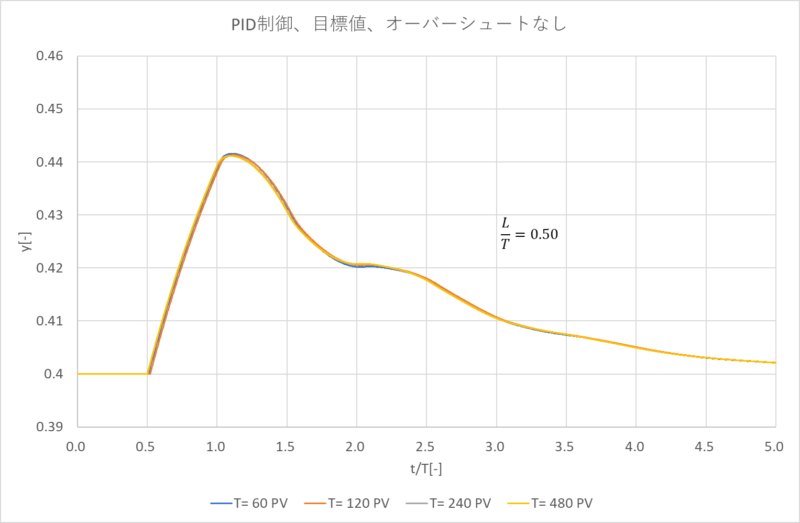
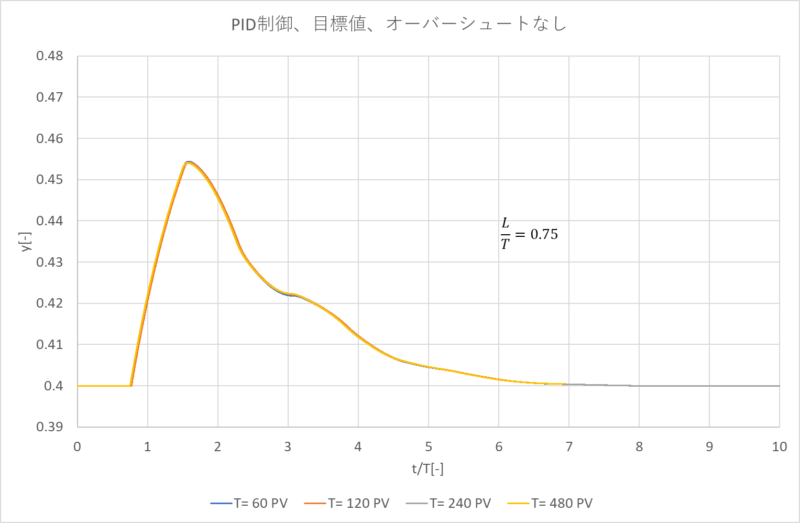
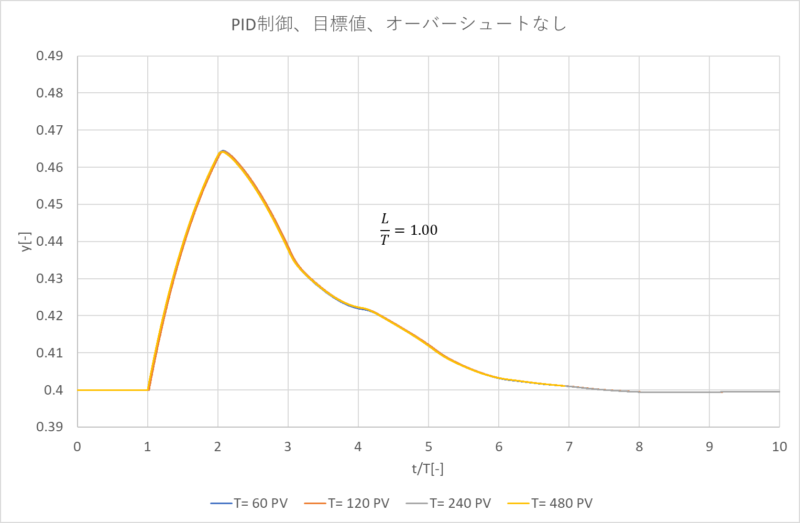
2-5.制御性の比較、確認
従って、制御性の比較、確認はプロセスの一次遅れの時定数\(T\)を一定とし、いくつかの\(\frac{L}/{T}\)でシミュレーションすることにより可能となる。
\(T=120\)、\(\frac{L}/{T}=0.25,0.5,0.75,1\)でのシミュレーション結果は下図のようになります。
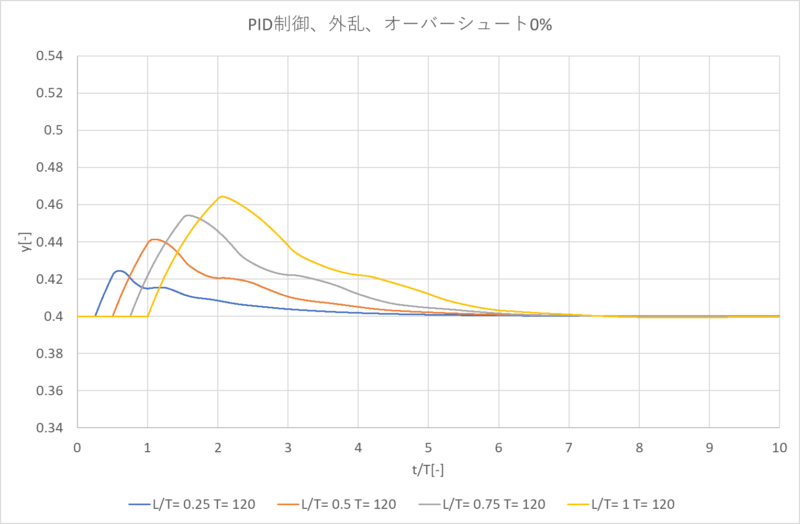
3.目標値変更、オーバーシュート0%、PI制御でのシミュレーション
次は、目標値変更、オーバーシュート0%、PI制御でのシミュレーションです。
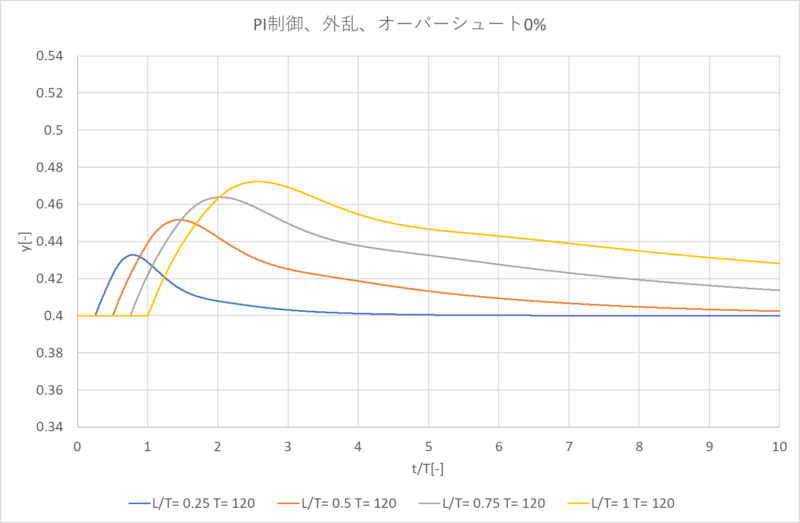
PID制御と同様に、\(T=120\)、\(\frac{L}/{T}=0.25,0.5,0.75,1\)でのシミュレーション結果を示します。
うまく制御できていることがわかると思います。
4.制御方法、オーバーシュートの比較
CHR法の調整法は制御方法(PID制御、PI制御)、オーバーシュート(0、20%)別になっています。
調整法の比較を$(T=240\)、\(L=60\)でシミュレーションを行った結果は下図のようになります。
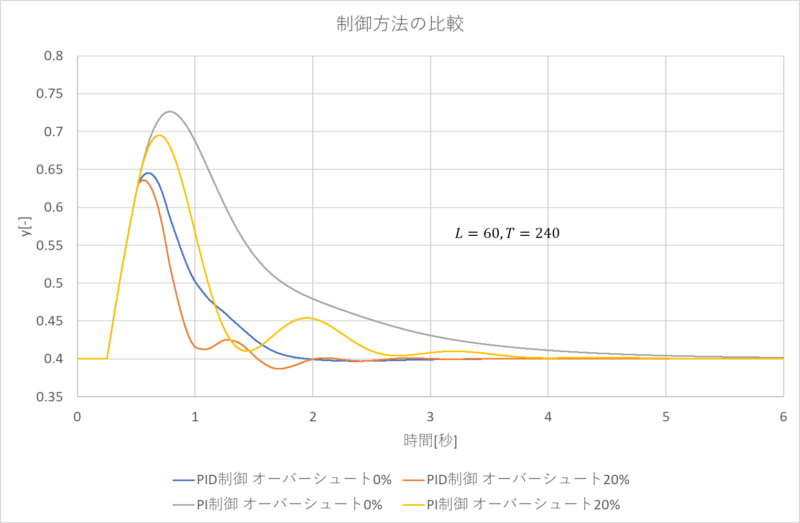
5.ロバスト性の確認
PID制御の特徴、長所として対象となるプロセスの動特性が想定と変わっても、ある程度制御できる点にあります。これを一般にロバスト性が高いといいます。
実際のプロセスでは、負荷の変動、性能(触媒能力、伝熱能力等)の変化によりプロセスの動特性は常に一定ではありません。このためロバスト性の高いPID制御が使われます。
ここでは、PID調節計のロバスト性をシミュレーションにより確認します。
下表のcase-0のプロセスの動特性でPID制御を目標値、オーバーシュート0%、PI制御でチューニングし、パラメータを決めます。
次に、case-1~case-7までプロセスの動特性を変化させ、制御状態を比較します。

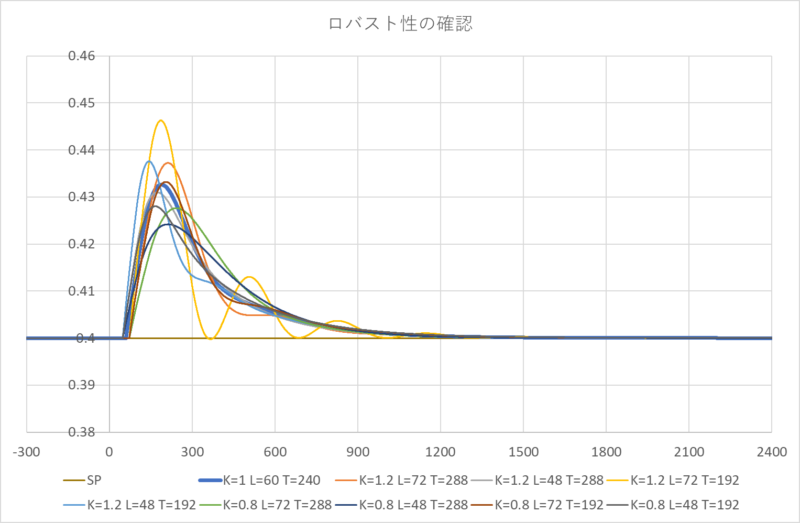
シミュレーションの結果を下図に示します。
\(K,L,T\)を0.8倍、1.2倍していますが、大きな乱れもなく制御できており、高いロバスト性を確認することができます。
6.制御方式による違い
PID制御には、比例、積分、微分すべての動作の入力が偏差であるPID制御、微分の入力が測定値である微分先行型PID制御(PI-D制御)、比例、微分の入力が測定値である比例微分先行PID制御(I-PD)制御があります。
DCSでは、PI-D、I-PD制御がよくつかわれているようです。
設定値変更では、それぞれで設定値変更時の挙動が違うため差が出ています。
外乱時には、設定値が一定のため、制御方法による差はみられません。(D操作を使用する、しないの差はあります。)
7.参考資料
広井和男,”ディジタル計装制御システムの基礎と応用”,工業技術社(1987)
橋本伊織、長谷部伸治、加納学, “新版プロセス制御工学”,朝倉書店(2020)