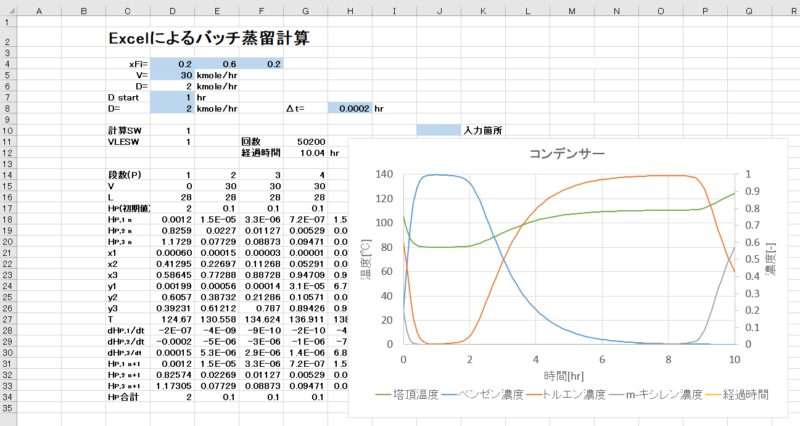
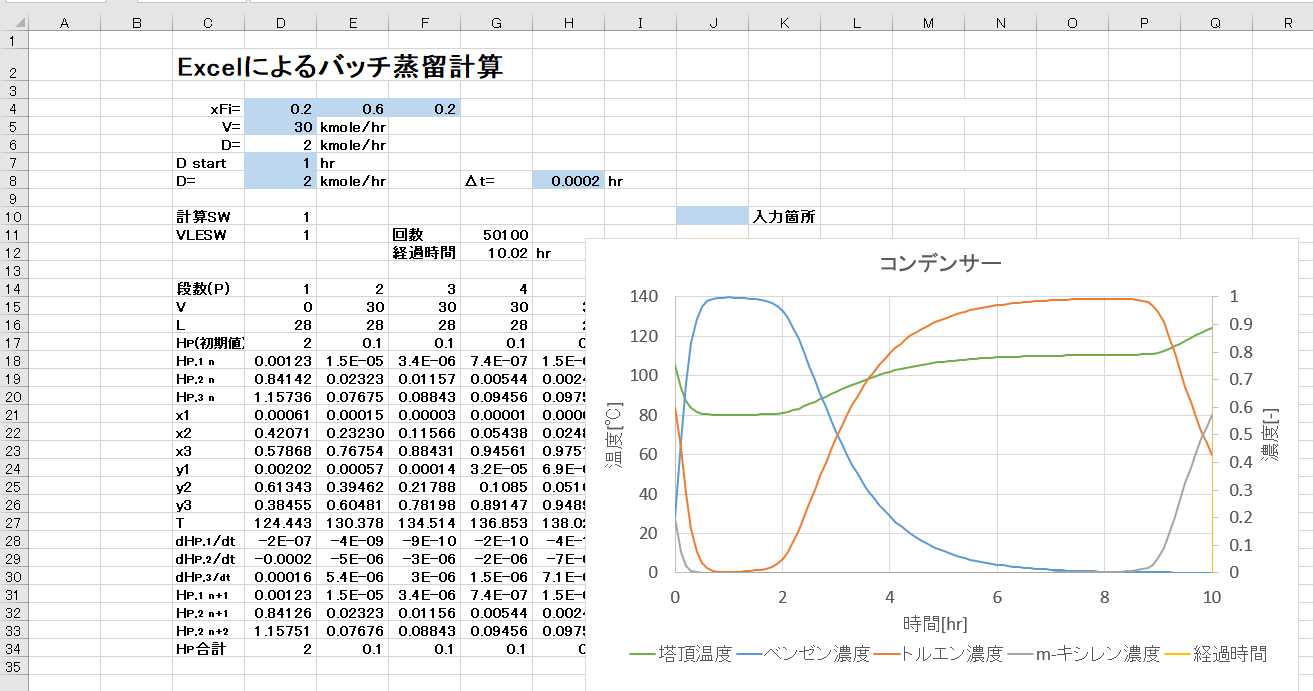
リラキゼーション法を用いた蒸留計算の例をバッチ蒸留に適用した事例を紹介します。
リラキゼーション法は、非定常状態から導かれた非線形微分方程式を解き、時間が無限大に達した時の解を求める手法であり、一種のダイナミックシミュレーションです。
従って、フィード、塔底抜出し、留出をやめた全還流運転を行い、その後に留出を開始することで、バッチ蒸留となります。
リラキゼーション法では最終的な定常状態が解として得られますが、バッチ蒸留では途中結果も重要になります。
このため、反復計算を利用して、バッチ蒸留計算で重要な途中結果を記録しています。
今回紹介するのは、ベンゼン(1) – トルエン(2) – m-キシレン(3)の3成分からなる理想系におけるバッチ蒸留計算です。この動画ではデモのため、時間がかかっていますが、実際の計算ではより短い時間で完了します。
1.バッチ蒸留塔の例
コンデンサー、リボイラーを含め理論段数10段でベンゼン(1) – トルエン(2) – m-キシレン(3)の3成分の分離を行う蒸留塔を例として使用します。
下記の仮定のもと計算を行います。
- 各成分のモル蒸発潜熱は等しく、従って各段の蒸気量、液量は一定とします。
操作条件
- 仕込み組成 \(x_{F,1}=0.2, x_{F,2}=0.6, x_{F,2}=0.2\)
- 留出量(D) 全館運転開始1時間後 \(2kmole/h\)
- 蒸気流量 \(30kmole/h\)
- 圧力 \(760mmHg\)
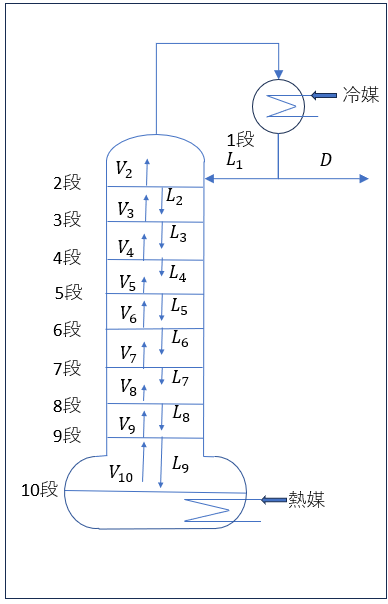
液量と蒸気量の関係
- \(V_2 = L_1 + D\)
- \(V_2=V_3=V_4=V_5=V_6=V_7=V_8=V_9=V_{10}\)
- \(L_1=L_2=L_3=L_4=L_5=L_6=L_7=L_8=L_9\)
2.気液平衡計算
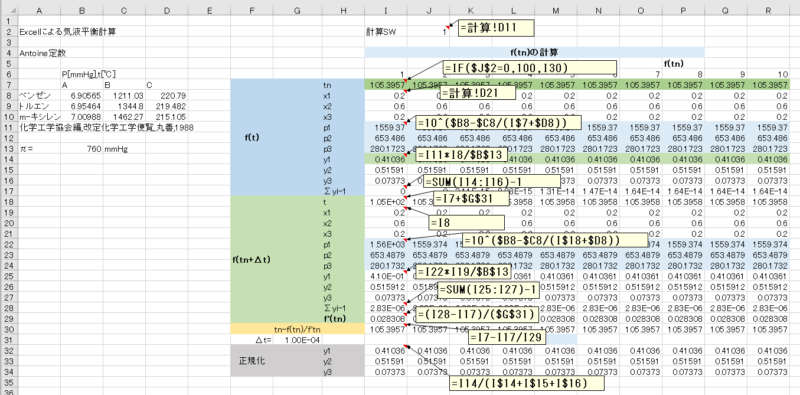
2-1. Excelによる3成分系の気液平衡計算
基本的には,2成分系の気液平衡計算と同じですが、最後に\(y_1 + y_2 + y_3=1\)となるようにノーマライズしています。
また、蒸留計算の段数が横方向となっているため、気液平衡計算もこれに合わせ段数を横方向としています。
3. バッチ蒸留計算
3-1. 物質収支式
各段の物質収支式からの非線形微分方程式は次のようになります。
リラキゼーション法と同じですが 、フィード段と塔底(10段)で\(F\)と\(W\)の項が無くなります。
- \(\frac{dH_{1,i}}{dt} = V_2 \cdot y_{2,i} – L_1 \cdot x_{D,i} – D \cdot x_{D,i} \)
- \(\frac{dH_{2,i}}{dt} = V_3 \cdot y_{3,i} + L_1 \cdot x_{D,i} – V_2 \cdot y_{2,i} – L_2 \cdot x_{2,i}\)
- \(\frac{dH_{3,i}}{dt} = V_4 \cdot y_{4,i} + L_2 \cdot x_{2,i} – V_3 \cdot y_{3,i} – L_3 \cdot x_{3,i}\)
- \(\frac{dH_{4,i}}{dt} = V_5 \cdot y_{5,i} + L_3 \cdot x_{3,i} – V_4 \cdot y_{4,i} – L_4 \cdot x_{4,i}\)
- \(\frac{dH_{5,i}}{dt} = V_6 \cdot y_{6,i} + L_4 \cdot x_{4,i} – V_5 \cdot y_{5,i} – L_5 \cdot x_{5,i}\)
- \(\frac{dH_{6,i}}{dt} = V_7 \cdot y_{7,i} + L_5 \cdot x_{5,i} – V_6 \cdot y_{6,i} – L_6 \cdot x_{6,i} \)
- \(\frac{dH_{7,i}}{dt} = V_8 \cdot y_{8,i} + L_6 \cdot x_{6,i} – V_7 \cdot y_{7,i} – L_7 \cdot x_{7,i}\)
- \(\frac{dH_{8,i}}{dt} = V_9 \cdot y_{9,i} + L_7 \cdot x_{7,i} – V_8 \cdot y_{8,i} – L_8 \cdot x_{8,i}\)
- \(\frac{dH_{9,i}}{dt} = V_10 \cdot y_{10,i} + L_8 \cdot x_{8,i} – V_9 \cdot y_{9,i} – L_9 \cdot x_{9,i}\)
- \(\frac{dH_{10,i}}{dt} = L_9 \cdot x_{9,i} – V_{10} \cdot y_{10,i} \)
3-2. ホールドアップ量
リラキゼーションによる連続蒸留計算では、最後の定常解のみが必要なため、塔のホールドアップ量は各所で同じとして計算しました。
しかし、バッチ蒸留計算では途中の結果が重要なため、実際に即したホールドアップ量とする必要があります。
ここでは下記のホールドアップ量を使用しています。
- コンデンサー \(2kmole\)
- 2~9段\(0.1kmole\)
- 塔底(缶) \(20kmole\)
ただし、塔底についてはバッチ蒸留が進むに従って減少するため、この値は初期値となります。
3-3. Excelによるバッチ蒸留計算
基本的にはExcelによるリラキゼーション法を3成分系にしたものになります。
Setp1
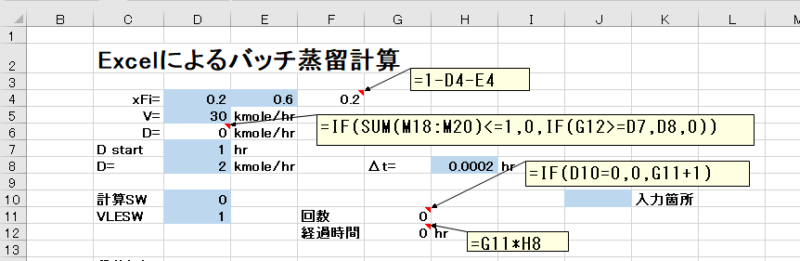
初めは操作条件の設定です。
- 仕込み組成 xFi の入力
- 蒸気量 V の入力
- 留出量 D
- 経過時間(G12)、留出開始時刻(D7)、留出量(D8)、10段ホールドアッップ量(sum(M18:M20))より計算
- =IF(SUM(M18:M20)<=1,0,IF(G12>=D7,D8,0))
- 計算SWの入力(D0,D11) 0でリセット、0以外で計算開始
- 刻み幅Δtの入力(H8)
- 回数の表示(G11)
- 計算SWが0以外となったら、反復計算時に1を加算
- =IF(D10=0,0,G11+1)
- 経過時間の表示(G12) =G11*H8
Step2
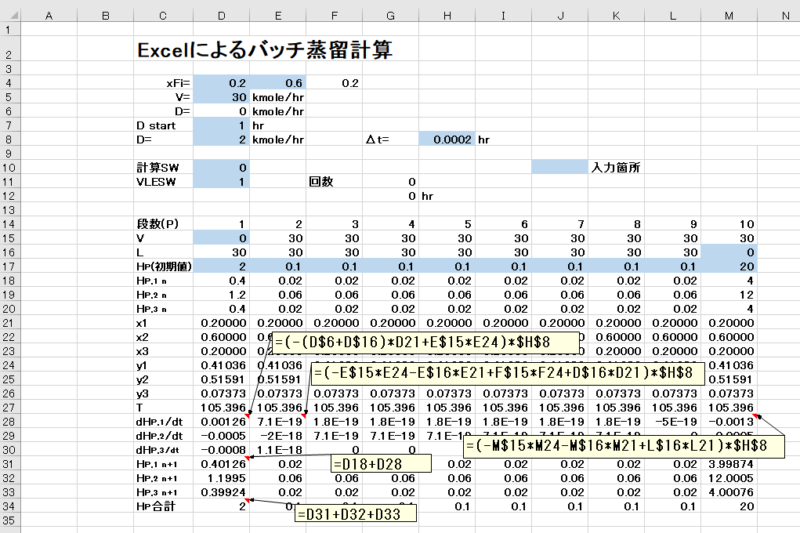
- 各段へのVの設定(E15~M15) =$D$5
- 各段へのLの設定(D16~L16) =$D$5-$D$6
- HP(初期値)の入力(D17~M17)
- HP,1,nの設定(D18) =IF($D$10=0,$D$4*D17,D31)
- 計算SW=0で、HP(初期値)×仕込み組成、計算SW=0以外でD31(HP,1,n+1)
- HP,2,n、HP,3,nにコピー、2~10段にコピ-
- x1の設定(D21) =D18/(D$18+D$19+D$20)
- x2,x3にコピー、2~10段にコピー
- y1の設定(D24) =気液平衡計算!I32
- y2,y3にコピー、2~10段にコピー
- Tの設定(D27) =気液平衡計算!I7
- 2~10段にコピー

Step3
- HP(=1),1,n/dtの設定(D28) =(-(D$6+D$16)*D21+E$15*E24)*$H$8
- D29,D30にコピ-
- HP(=2),1,n/dtの設定(E28) =(-E$15*E24-E$16*E21+F$15*F24+D$16*D21)*$H$8
- E29,E30にコピ-、3~9段にコピー
- HP(=10),1,n/dtの設定(M28) =(-M$15*M24-M$16*M21+L$16*L21)*$H$8
- M29,M30にコピー
- HP,1,n+1の設定(D31) の設定 =D18+D28
- D32,D33にコピー、2~10段にコピー
4. 途中経過の記録
バッチ蒸留では、途中の経過が重要となります。
ここでは、反復計算を利用して途中経過の記録を行います。
4-1. 記録方法
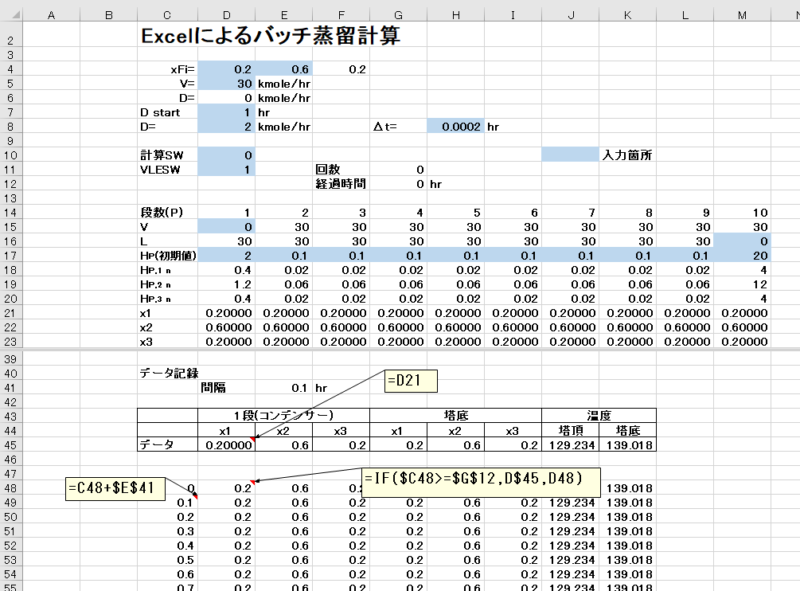
- 1段目のx1(D21)を記録する場合で説明します。
- D41に=D21と設定し、1段目のx1を表示します。
- E41に記録する間隔を入力します。この場合は0.1hrです。
- C48に0を入力し、C49に=C48+$E$41と設定し、記録したい時間分だけ下にコピーします。
- D48に下記式を設定し、下にコピーします。
- =IF($C48>=$G$12,D$45,D48)
- この式の意味は、記録を残したい時刻($C48)が現在の経過時間($G$12)より大きい場合、すなわちまだその時間になっていない場合は、現在の値(D$45)とし、経過時間以上になったら、現在表示している値(D48)をそのまま保持します。
これにより、その時間の値を記録することが可能となります。
5. Excelによるバッチ蒸留計算の完成
以上により、Excelによるバッチ蒸留計算が出来ました。
計算SWを1に切り替え、反復計算を50000回行うことにより10時間の経過が計算出来ます。