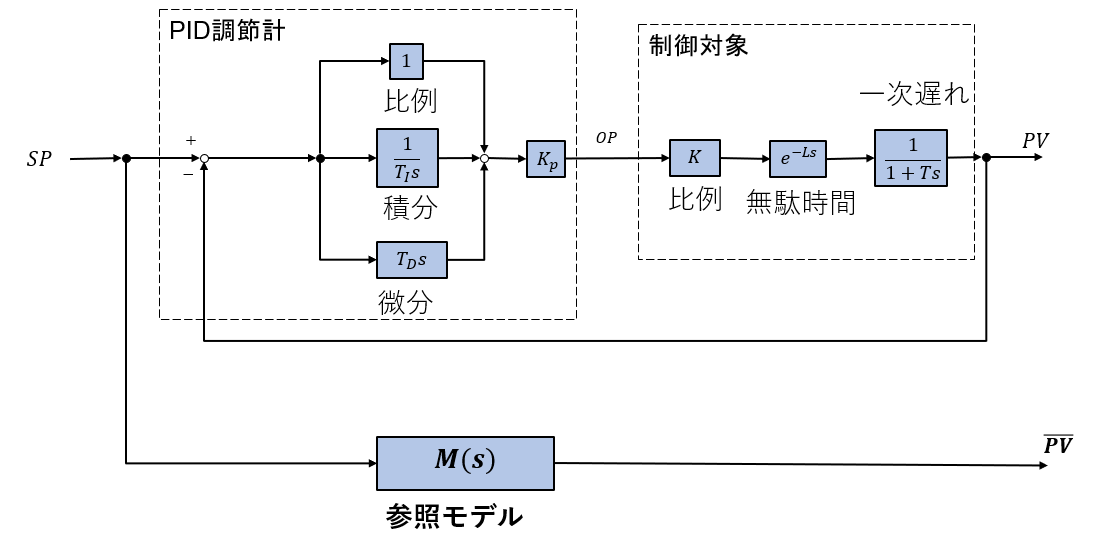
先に紹介した”ExcelによるPID制御のチューニング(1)では、無駄時間+一次遅れのプロセスに対して、CHR法でのチューニングを紹介しました。
ここでは、Excelを使った参照モデルを使ったチューニング方法を紹介します。
1.参照モデルを使ったチューニング法
参照モデルを使ったチューニングとは、下記のブロック線図で指示値(\(PV\))に参照モデルの出力(\(\overline{PV}\))を一致(マッチング）させるという方法です。
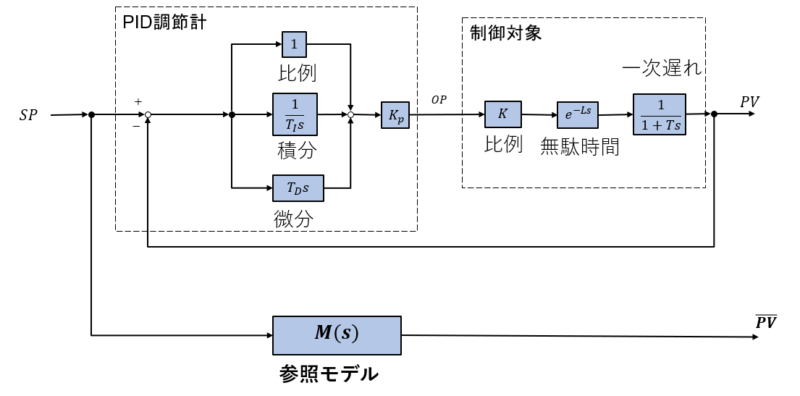
参照モデルとしては、PI-D制御では2次遅れ、I-PD制御では3次遅れをここでは使用します。
また、上記ブロック線図からわかるように指示値(\(PV\))は無駄時間要素を含みます。したがって、参照モデルにも無駄時間\(L_M\)が必要となり、それぞれ無駄時間+2次遅れ、無駄時間+3次遅れとします。ただし、参照モデルの無駄時間とプロセスの無駄時間は同じではありません。
次に、参照モデルの時定数を決める必要がります。時定数は下記の式でから求めます。
\(\tau=\frac{T_{99}}{4.4n^{0.6}}\)
ここで\(T_{99}\)は、99%となる応答時間で、\(n\)は次数になります。
2.チューニングの手順
チューニングの手順は下記の通りです。
- 対象プロセスのゲイン、無駄時間、１次遅れ時定数を入力します。（対象プロセスの設定）
- 制御方法(PI-D、I-PD)を選択します。
- 希望する整定時間を入力します。
- 参照モデルの無駄時間(\(L_M\))の初期値を入力します。
- 希望する整定時間と参照モデルの無駄時間から\(T_{99}\)を計算します。
- 制御方式及び\(T_{99}\)から参照モデルの時定数を計算します。
- P,I,Dパラメータの初期値を入力し、\(PV\)を計算します。
- 参照モデルと設定値(\(SP\))より、\(\overline{PV}\)を計算します。
- \(\Sigma=(PV-\overline{PV})^2\)を最小とする、PIDパラメータ及び参照モデルの無駄時間(\(L_M\))を求めます。
3.Excelシートの変更
先に紹介した”ExcelによるPID制御のシミュレーション(2)”のワークシートを使います。
3-1.PIDパラメータ、プロセスの動特性の入力
ここでは、例として下図のように入力します。
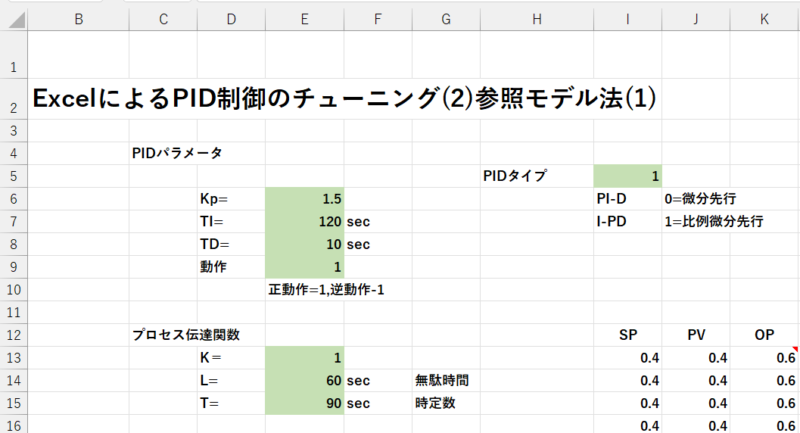
PIDタイプは、I-PD(比例微分先行)で正動作です。PIDパラメータは、初期値となります。
プロセスは無駄時間+1次遅れです。
3-2.整定時間、無駄時間の入力および参照モデルの時定数の計算
希望する整定時間と無駄時間(\(L_M\),初期値)を入力します。
参照モデルの時定数は、下記の式を入力します。
\(\tau=\frac{T_{99}}{4.4n^{0.6}}\)
ここで\(T_{99}\)は、(整定時間-無駄時間)で、\(n\)は次数になります。
3-3.参照モデルの計算
参照モデルは、PI-D制御の時2次遅れ、I-PD制御の時3次遅れとなり、これに無駄時間を加え、最大で無駄時間+3次遅れ系となります。
下図のように、無駄時間と三つの1次遅れを貼り付け、式を入力します。
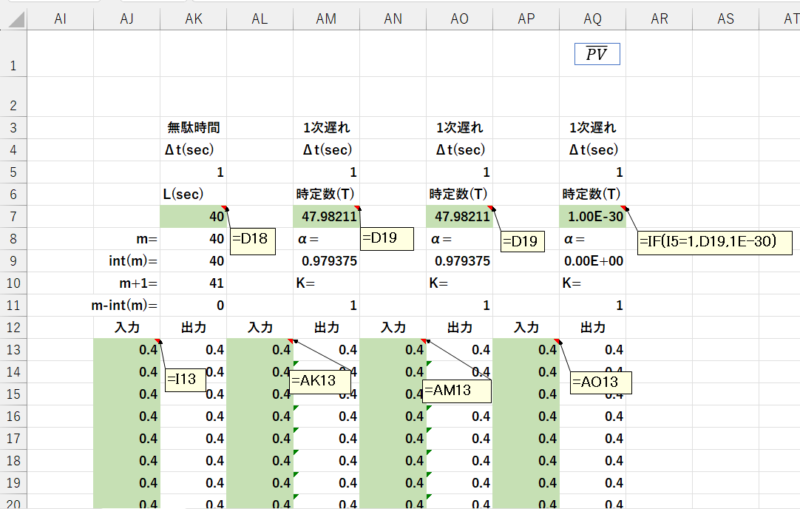
- AJ13には、SP(I13)が入ります。
- AK7には、無駄時間(D18)が入ります。
- AM7、AO7には、時定数(D19)が入ります。
- AQ7には、I-PD制御の時は時定数(D19)が、PI-Dの時には、ゼロに近い(1e-30)hが入ります。
これにより2次遅れと、3次遅れを切り替えています。 - 1次遅れの入力は、左側のセルとなります。
3-4.\(PV\)と\(\overline{PV}\)の誤差最小
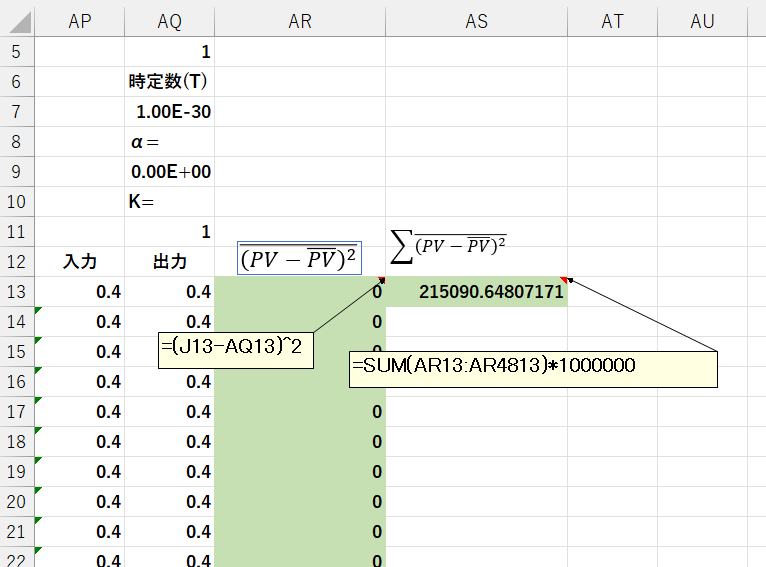
\(PV\)と\(\overline{PV}\)との誤差の2乗の合計を下図のようにして計算します。
これがソルバーの目的セルになります。
収束の状況をわかりやすくするため、1e6をかけています。
3-5.ソルバーによる最適化
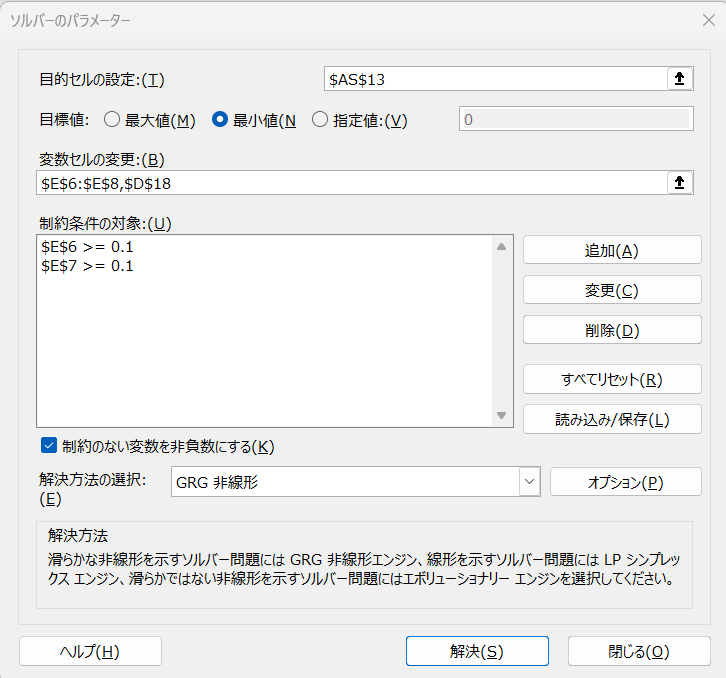
最適なP,I,Dパラメータおよび参照モデルの無駄時間(\(L_M\))をソルバーにより見つけます。
Kp,TIに関しては,ゼロとならないような制約要件をつけます。
4.チューニングの例
下記のプロセスの伝達関数の系でチューニングを行った例を示します。
プロセス伝達関数
K＝ 1 (ゲイン)
L= 150 sec (無駄時間)
T= 300 sec (時定数)
整定時間を600～1080秒でチューニングを行っています。
結果は下記の通りです。
4-1.整定時間とΣ誤差2乗
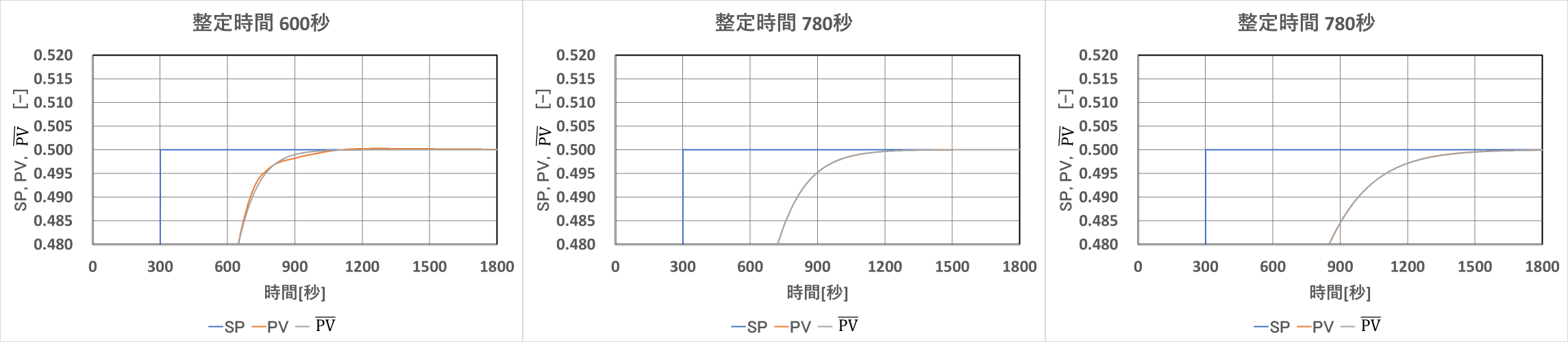
整定時間を変えるとΣ誤差2乗も変化します。整定時間により、参照モデルとのズレが変化することになります。
整定時間とΣ誤差2乗の関係は下図のようになります。
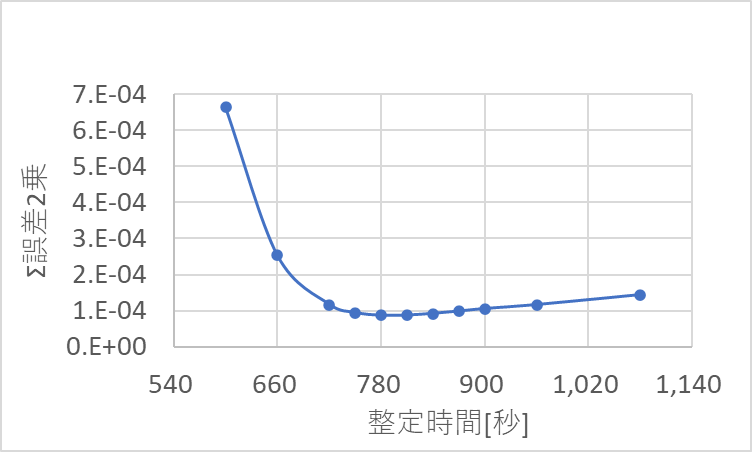
整定時間780秒で、Σ誤差2乗は最初となり、それ以上では緩やかに上昇し、それ以下になると急激に上昇します。
最適な整定時間を超えても、参照モデルとのズレは少ないですが、それ以下になるとズレが急激に増加することになります。
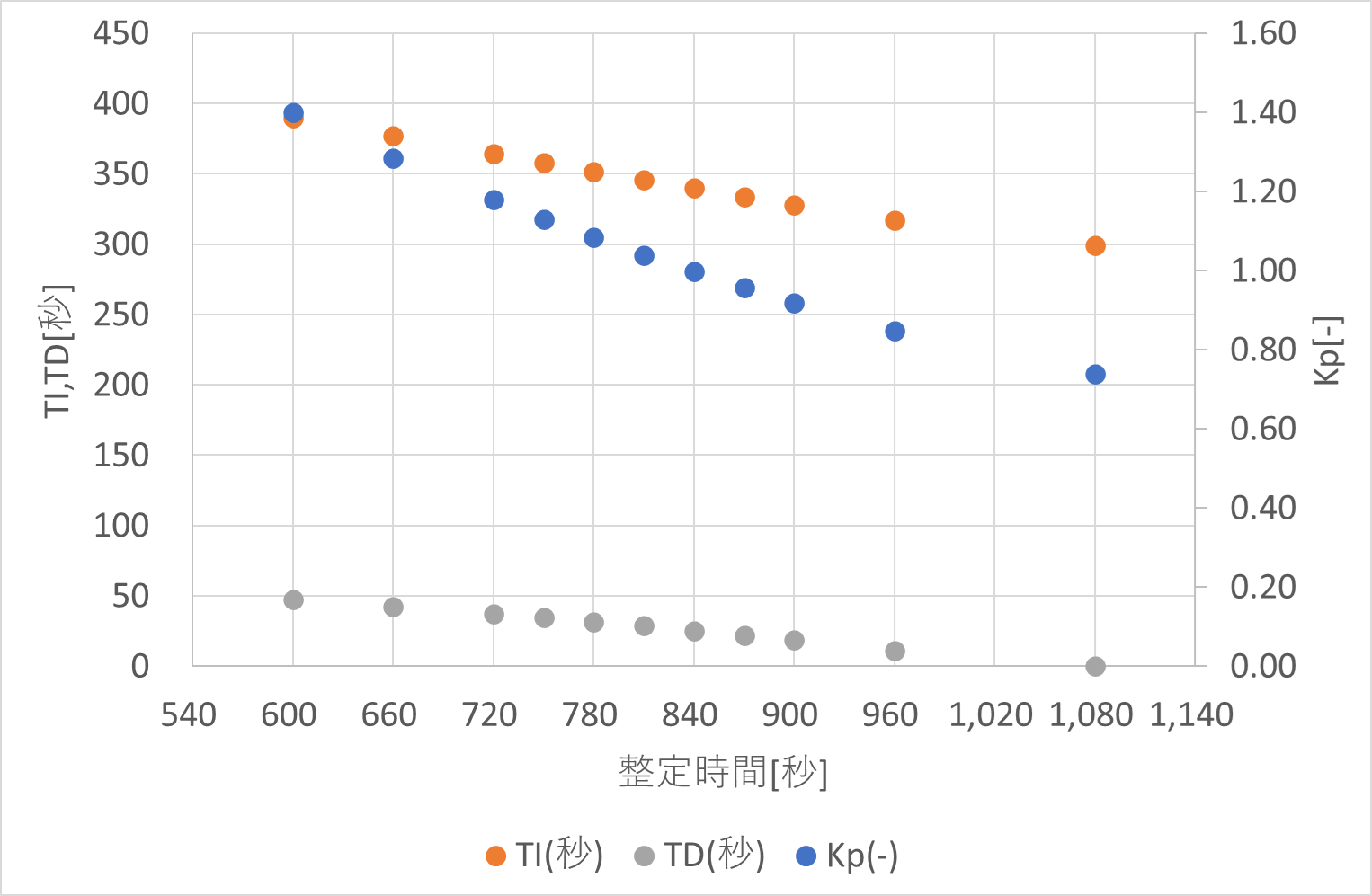
4-2.整定時間とP,I,Dパラメータ
整定時間とP,I,Dパラメータの関係をグラフにしてみます。
いずれも、整定時間が長くなるほど小さくなることがわかります。
5.参考資料
参照モデルの詳細および参照モデルに無駄時間を加えることなど、下記資料を参考とさせていただきました。
加納，小河，田坂，高橋，滝波，吉井，大寶，増田：モデル不要PID調整法E-FRITの開発と実用化，計測と制御，50–12,1076/1079 (2011)
次回(2025年1月)は、上記の”モデル不要PID調整法E-FRIT”のExcelでのシミュレーションを紹介する予定です。