PIDのチューニングの代表的な方法としてCHR法があります。
この方法では、対象プロセスを無駄時間+一次遅れ系に近似し、ゲイン\(K\)、無駄時間\(L\)、一次遅れの時定数\(L\)から、P,I,Dのパラメータを計算します。
\(P(s) = \)\(\frac{K}{1 + Ts}\) \(e^{-Ls}\)
今回は、対象プロセスを無駄時間+一次遅れ系に近似する方法を紹介します。
1.疑似プロセスモデル
無駄時間+一次遅れ系に近似する疑似プロセスモデルを、次の5次遅れ系とします。
\(P(s) =\)\(\frac{1}{(1 + T_1 s)(1 + T_2 s)(1 + T_3)(1 + T_4 s)(1 + T_5 s)}\)
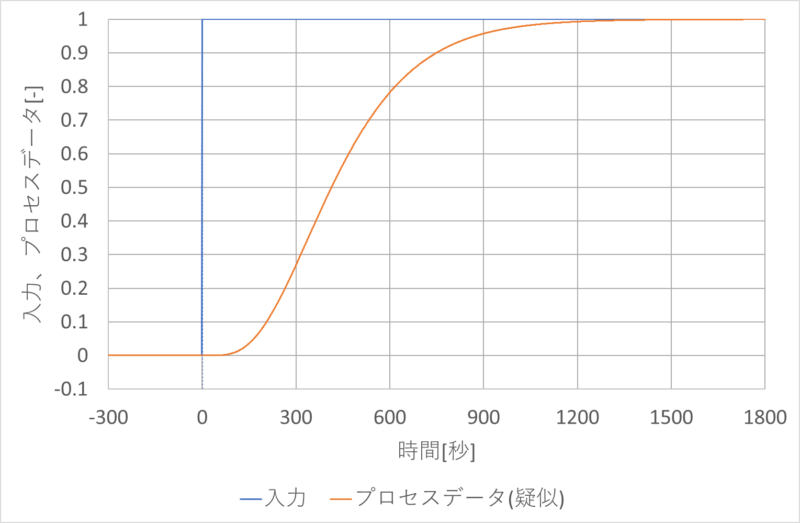
ステップ応答は下図のとおりです。
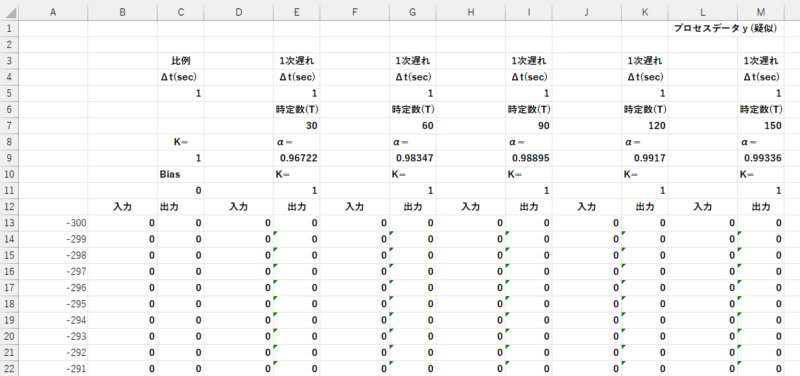
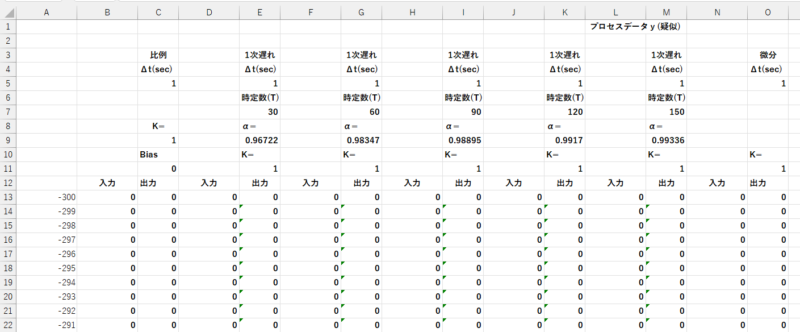
Excelでは、”Excelによる伝達関数の計算”で紹介した、比例、一次遅れの伝達関数を使い疑似プロセスを構築します。
各一次遅れの入力は、前の伝達関数の出力です。
2.接線法
無駄時間、一次遅れの時定数を求める方法の一つに接線法があります。
下図のように、変曲点(微分値が最大となる点)を求め、この点を通る接線を引きます。
この線とy=0の交点までの時間が無駄時間\(L\)となり、y=1の交点までの時間から無駄時間を引いた値が一次遅れの時定数\(T\)となります。
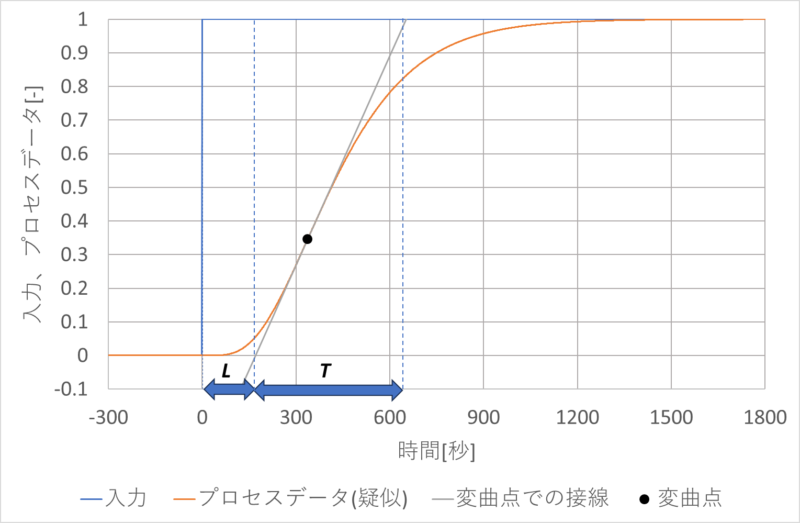
変曲点は、微分値が最大となる点で、Excelでは微分の伝達関数を追加することにより見つけることができます。
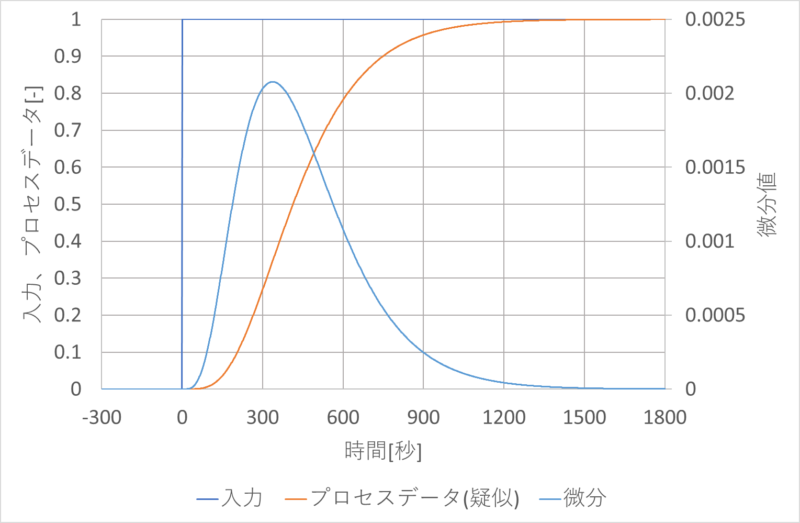
この例では、微分値最大(傾き)0.00208、時間 337 秒、その時のy=0.3457となり、この値から、変曲点での接線の式は \(y=0.002077t-0.3543\)となります。
この式から\(L=170.6\)秒、\(T=481.4\)秒が計算されます。
3.2点法
次は、2点のデータから無駄時間\(L\)、一次遅れの時定数\(T\)を求める方法です。
\(y\)の値が85.3%となる時間\(t_{85.3\%}\)と35.3%となる時間\(t_{35.3\%}\)を使います。
この値より次式により、無駄時間\(L\)、一次遅れの時定数\(T\)が求まります。
\(T = 0.67(t_{85.3\%} – t_{35.3\%})|\)
\(L=1.3t_{35.3\%} – 0.29t_{85.3\%}\)
これは、一次遅れの微分方程式の解析解 \(y = 1 – e^{-(t-L)/T}\)から導き出されます。
同様に、次の式からも求めることができます。
\(T = 1.5(t_{63.2\%} – t_{28.3\%})|\)
\(L=1.5t_{28.3\%} – 0.5t_{63.2\%}\)
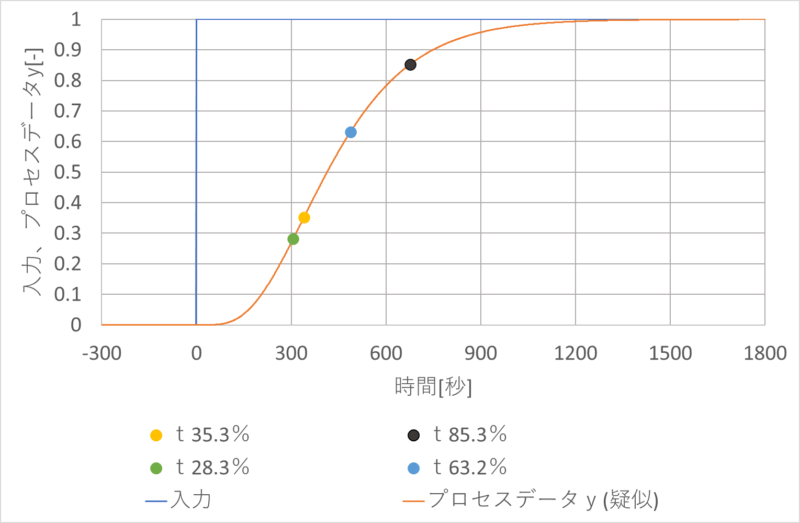
1.疑似プロセスモデルのExcelシートに下記のように加えると、\(t_{85.3\%}\)などが簡単に計算でき、\(T,L\)も求めることができます。
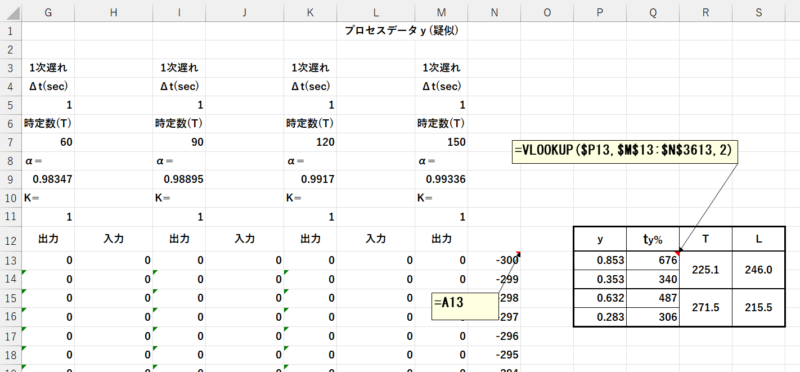
4.最小二乗法
接線法、2点法は、データ(グラフ)が紙で与えられた時は、便利で簡便な方法です。
しかし、DCS等のデジタル機器が広く使用されている現在においては、プロセスデータはExcel等に簡単に変換することができます。
このような場合は、最小二乗法により無駄時間\(L\)、一次遅れの時定数\(T\)を求める方法が便利です。
プロセスデータを\(y\)、無駄時間+一次遅れで計算した値を\(y_{cal}\)とし、これらの値の差の二乗の合計\(\sum (y – y_{cal})^2\)を最小とする無駄時間\(L\)、一次遅れの時定数\(T\)を求める方法です。
1.疑似プロセスモデルのExcelシートを使用します。
- 新しく無駄時間と一次遅れの伝達関数を追加します。
- 無駄時間の伝達関数の入力はプロセスデータの入力(B13)です。
- 一次遅れの伝達関数の入力は無駄時間の出力です。
- S列で\((y – y_{cal})^2\)を計算し、U12で合計を計算します。
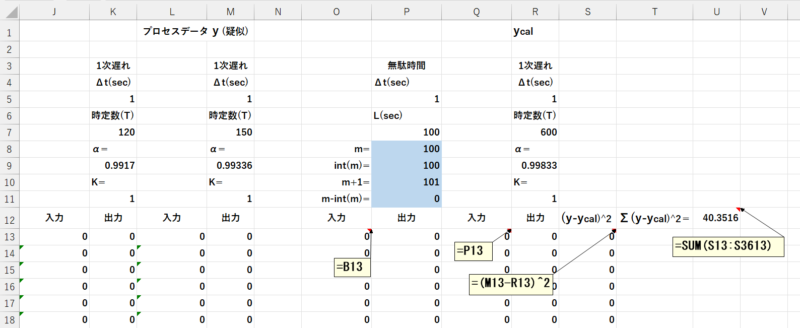
この合計を最小とする無駄時間\(L\)、一次遅れの時定数\(T\)を見つけるのにはソルバーを使用します。
- 目的セルの設定は、合計値($U$12)とします。
- 目標値は最小値です。
- 変数セルの変更は、無駄時間\(L\)($P$7)、一次遅れの時定数\(T\)($R$7)です。
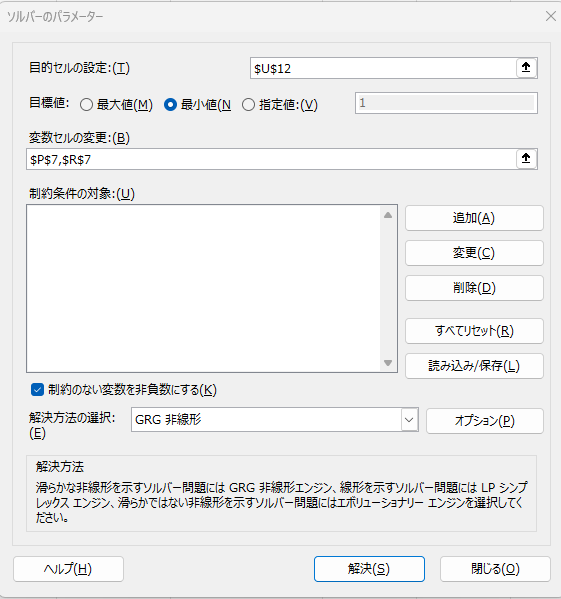
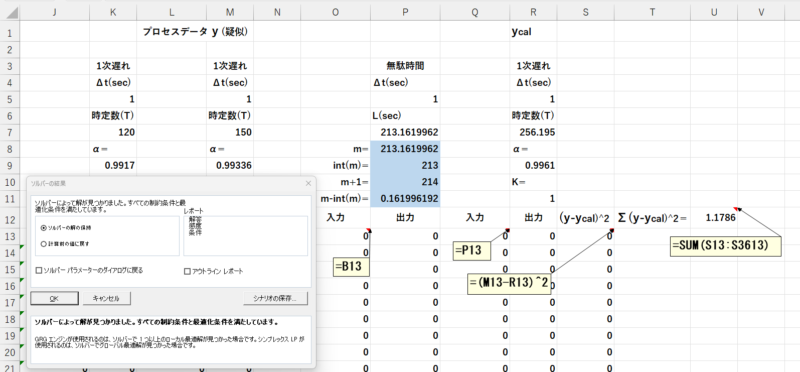
解決のボタンを押せば、最小となる値を計算してくれます。
この式から\(L=213.2\)秒、\(T=256.2\)秒が計算されます。
この式から\(L=170.6\)秒、\(T=481.4\)秒が計算されます。
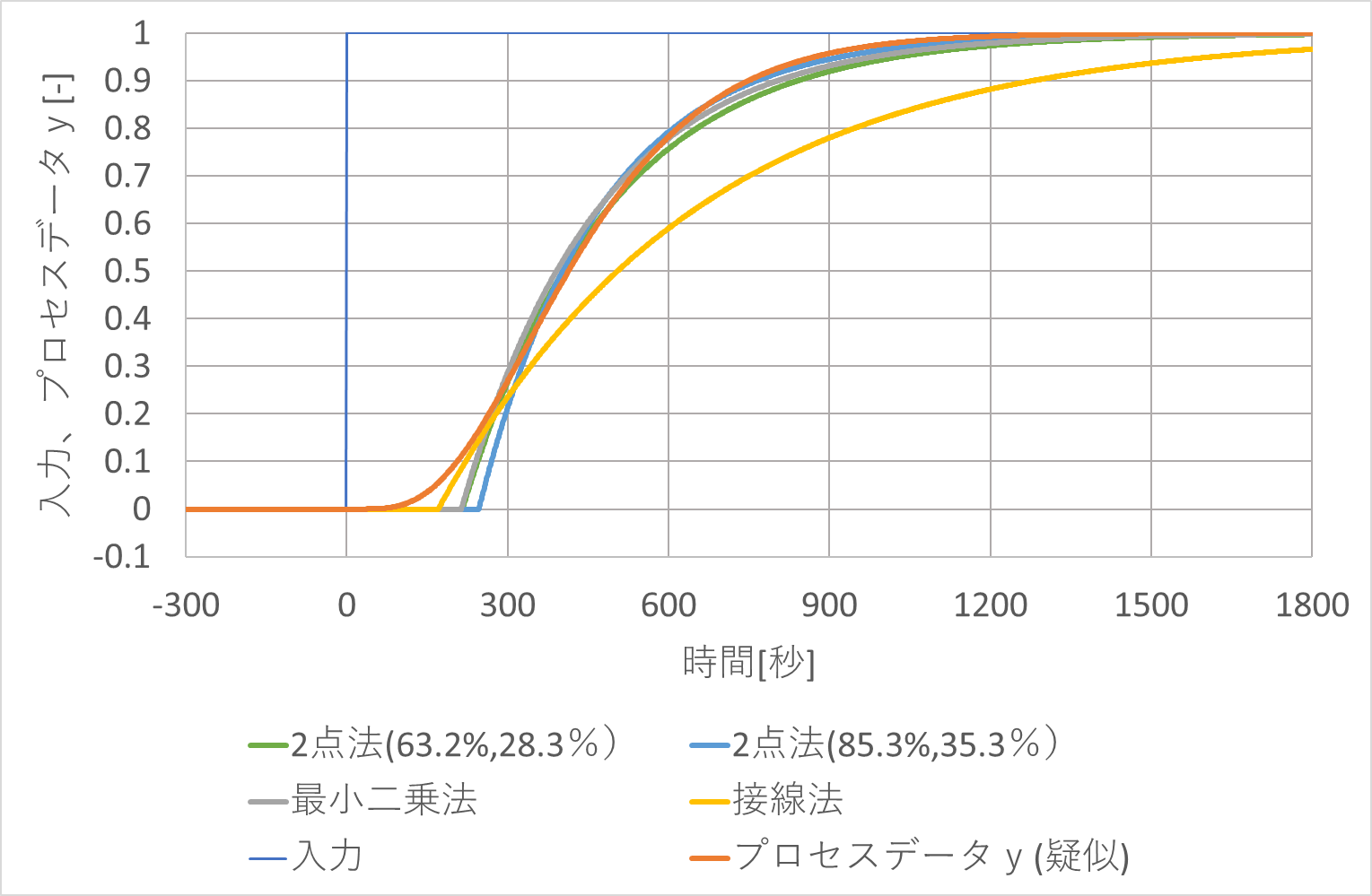
5.各手法の比較
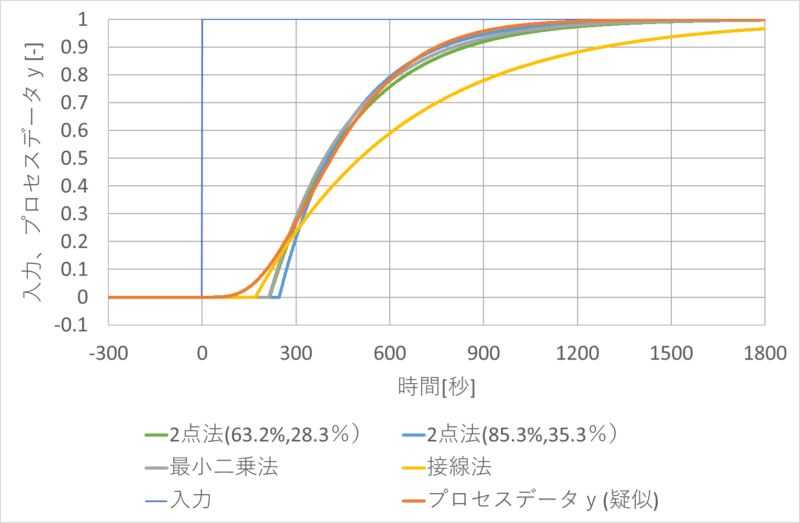
各手法で求めた無駄時間\(L\)、一次遅れの時定数\(T\)でシミュレーションした結果を下記に示します。
接線法は、1点(変曲点)の情報から求めた値であり、精度にかける場合があります。
2点法、最小2乗法はほぼ同等の精度があることがわかります。
6.無駄時間+2次遅れ系
プロセスデータを無駄時間+1次遅れ系でモデル化した例を紹介しましたが、立ち上がりの部分がうまく表現できないのが問題になることもあります。
この場合は、無駄時間+2次遅れ系でモデリングするのも一つの方法かと思います。
\(P(s) =\)\( \frac{1}{{(1 + Ts)(1 + Ts)}}\) \(e^{-Ls}\)
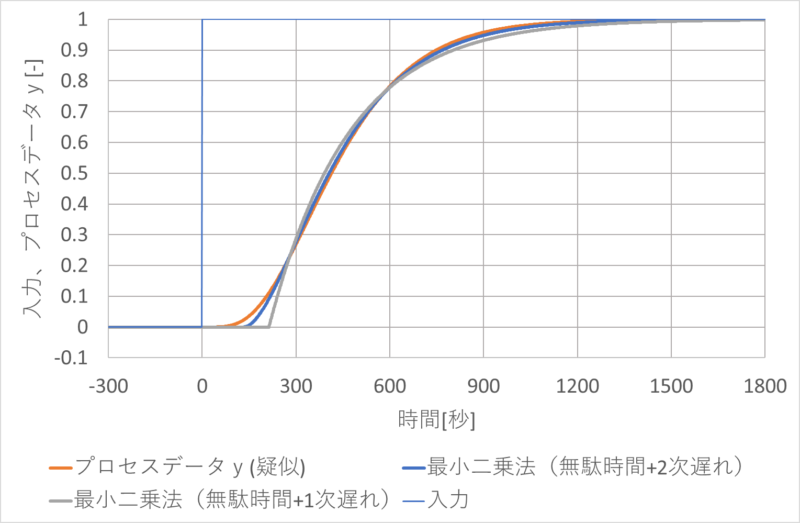
下記は、無駄時間+1次遅れ系と無駄時間+2次遅れ系の比較です。
無駄時間+2次遅れ系でモデリングすることにより、より精度が上がることがわかると思います。
7.参考資料
広井和男,”ディジタル計装制御システムの基礎と応用”,工業技術社(1987)
橋本伊織、長谷部伸治、加納学, “新版プロセス制御工学”,朝倉書店(2020)