ここでは、Excelを使った伝達関数の計算を紹介します。
この計算を組み合わせることにより、PID制御のシミュレーション等が行えます。
1.プロセス制御とPID制御
化学工業などのプロセス産業での制御をプロセス制御と言います。プロセス制御では、様々な制御システムが使用されていますが、その90%以上でPID制御が使用されていると言われています。PID制御では、比例、積分、微分の3つのパラメータにより様々な対象物での制御を可能としています。
従って、PID制御を理解し使いこなすことがプロセス制御では重要となります。
2.PID制御とブロック線図、伝達関数
PID制御では、下のような図が出てきます。
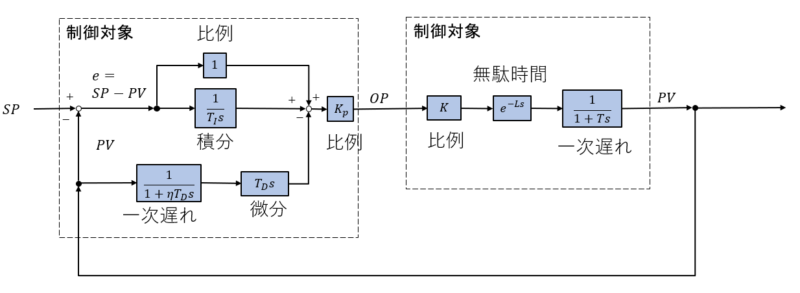
この図をブロック線図と言い、青色四角の中の数式が伝達関数です。ブロック線図は、信号の流れを表しています。
設定値(\(SP\))とプロセスの値(\(PV\))との差を偏差と言いeで表します。この偏差(\(e\))に比例、積分、微分処理を行い、更に比例処理を行ったものがPID調節計の出力(\((OP\))となります。
制御対象は、比例、無駄時間、一次遅れで表現されることが多い様です。
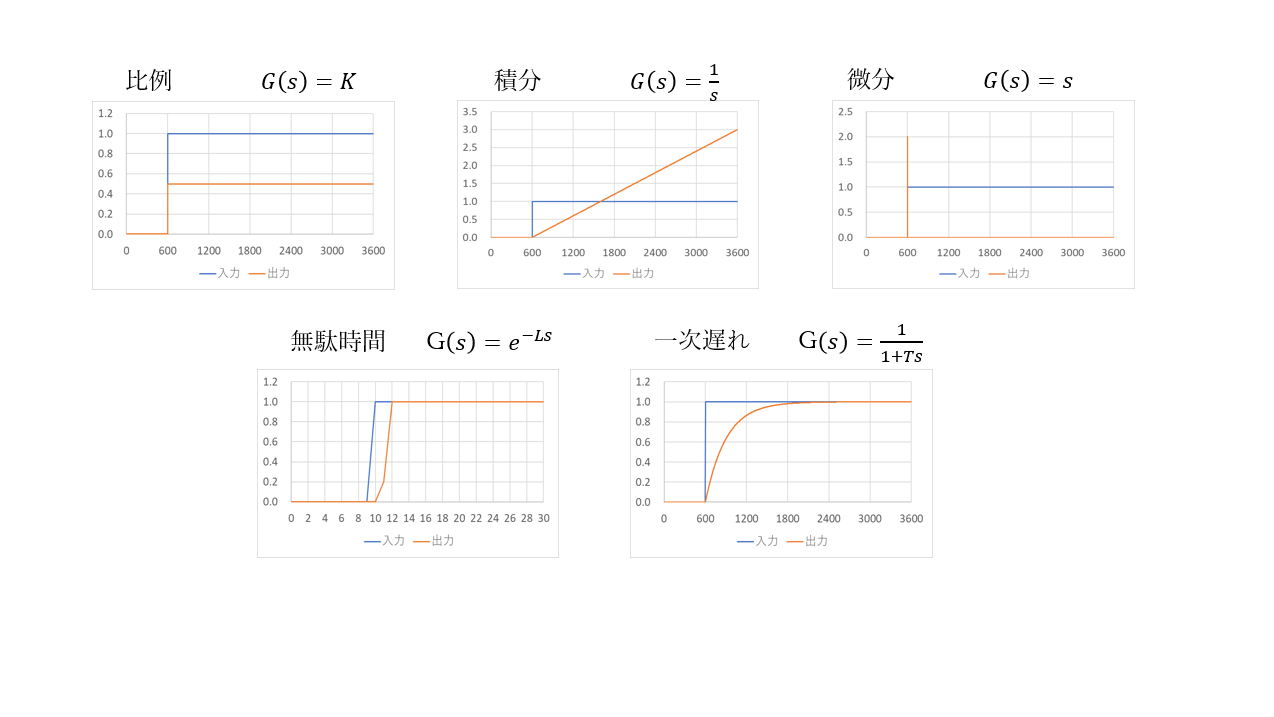
従って、下記の五つの伝達関数があれば、プロセスを含めたPID制御の簡単なシミュレーションを行うことができます。
- 比例 \(G(s) = K\)
- 積分 \(G(s) = \frac{1}{s}\)
- 微分 \(G(s) = s\)
- 無駄時間 \(G(s) = e^{-Ls}\)
- 一次遅れ \(G(s) = \frac{1}{1+Ts}\)
3 Excelによる伝達関数の計算
3-1 比例の伝達関数
Excelで伝達関数を計算するには、刻み幅\(\Delta t\)を使って離散化します。
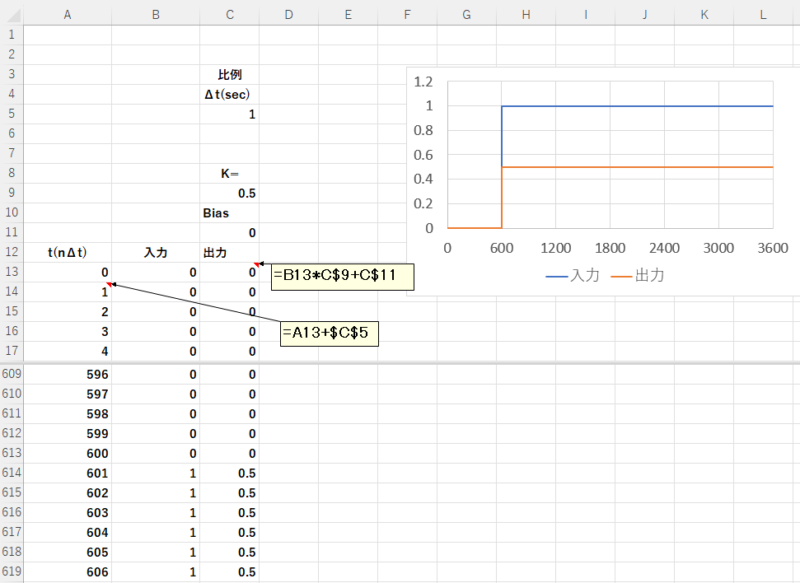
比例の伝達関数\(G(s) = K\)は、次式で表せます。
\(y_n = K x_n\)
Excelでは次のように入力します。
- C5
\(\Delta t\)を入力します。 - A列
時間 \(t(n\Delta t)\)を入力します。
上の行の値 + \(\Delta t\) - B列
入力値を入力します。
この場合、601秒に0から1に変わります。 - C列
9行目は\(K\)、11行目は\(Bias\) を入れます。
13行目以下は、出力の計算式を入力します。
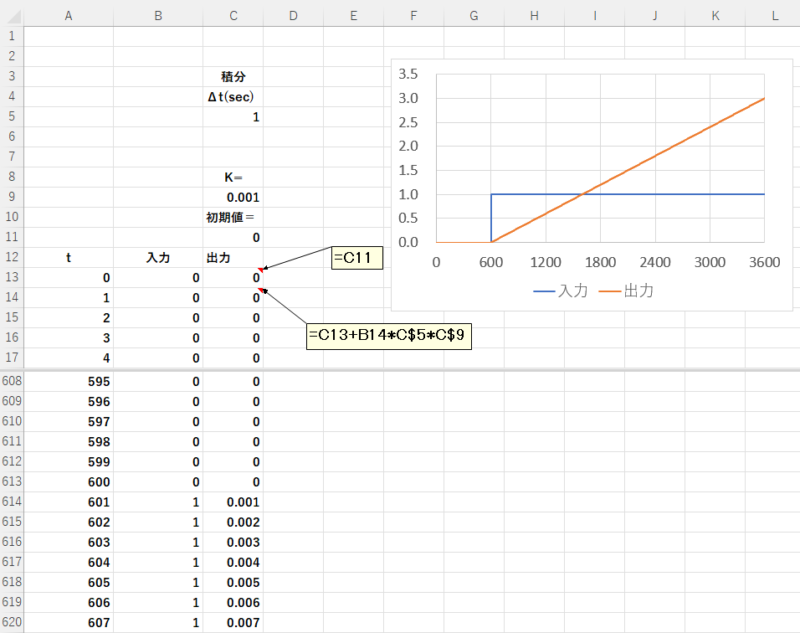
3-2 積分の伝達関数
積分の伝達関数\(G(s) = \frac{1}{s}\)は、次式で表せます。(比例定数\(K\)を含みます。)
\(y_n = y_{n-1} + Kx_n \cdot \Delta t\)
Excelでは次のように設定します。
- C5
\(\Delta t\)を入力します。 - A列
時間 \(t(n\Delta t)\)を入力します。
上の行の値 + \(\Delta t\) - B列
入力値を入力します。
この場合、601秒に0から1に変わります。 - C列
9行目は\(K\)、11行目は初期値を入力します。
13行目以下は、出力の計算式を入力します。
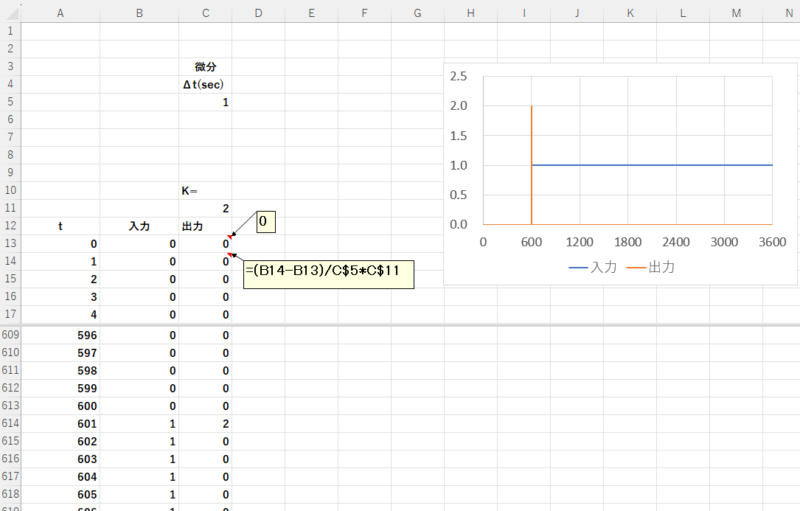
3-3 微分の伝達関数
微分の伝達関数\(G(s) = s\)は、次式で表せます。(比例定数\(K\)を含みます。)
\(y_n = K \frac{{x_n – x_{n-1}}}{{\Delta t}}\)
Excelでは次のように設定します。
- C5
\(\Delta t\)を入力します。 - A列
時間 \(t(n\Delta t)\)を入力します。
上の行の値 + \(\Delta t\) - B列
入力値を入力します。
この場合、601秒に0から1に変わります。 - C列
11行目は\(K\)を入力します。
13行目以下は、出力の計算式を入力します。
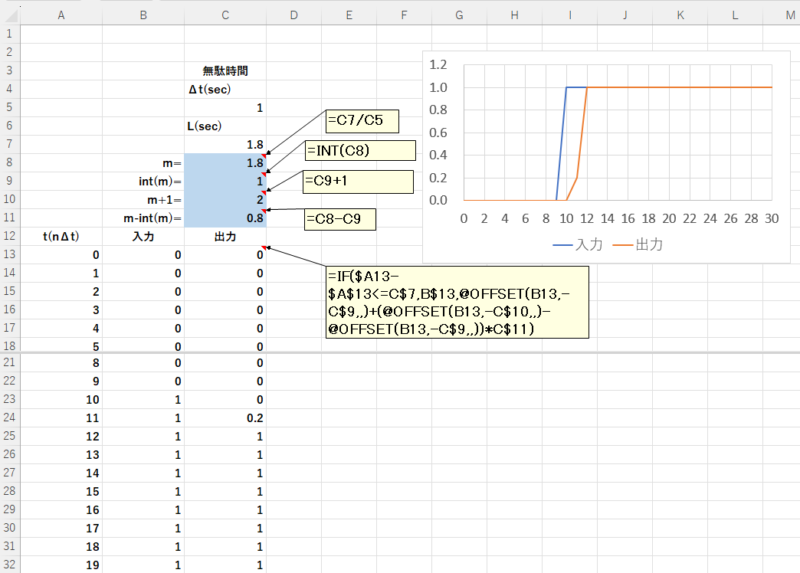
3-4 無駄時間の伝達関数
無駄時間の伝達関数\(G(s) = e^{-Ls}\)は、次式で表せます。
\(y_n = x_{n-m}\)
\(m = Ls / \Delta t\)
Excelでは次のように設定します。
なお、\(m = Ls / \Delta t\)が整数でない場合にも計算できるようにしています。これは、ソルバーの変数セルとして使用する場合を想定してのことです。
- C5
\(\Delta t\)を入力します。 - A列
時間 \(t(n\Delta t)\)を入力します。
上の行の値 + \(\Delta t\) - B列
入力値を入力します。
この場合、10秒に0から1に変わります。 - C列
7行目は無駄時間\(Ls\)を入力します。
8行目で、\(m = Ls / \Delta t\)を計算し、9行目が\(m\)の整数部分、10行目が整数部分+1、10行目が\(m\)の小数部分になります。
13行目以下は、出力の計算式を入力します。
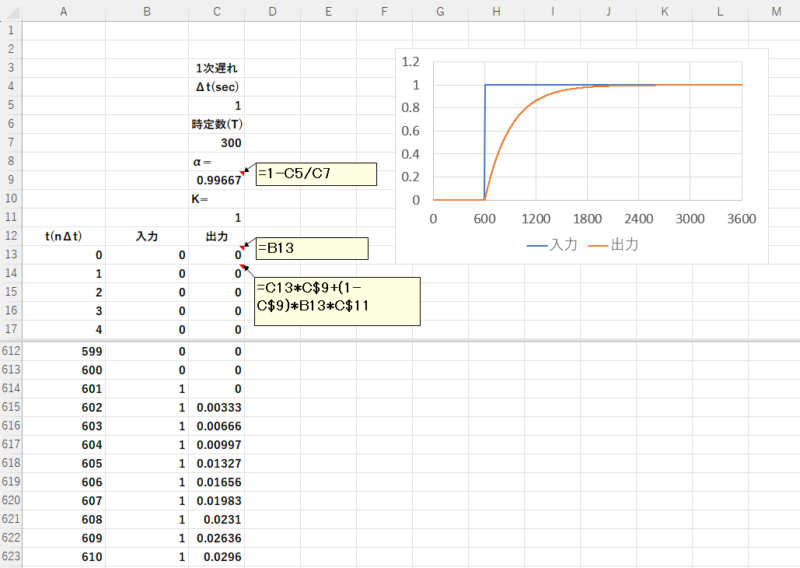
3-5 一次遅れの伝達関数
一次遅れの伝達関数\(G(s) = \frac{1}{1+Ts}\)は、次式で表せます。(比例定数\(K\)を含みます。)
\(y_n = \alpha y_{n-1} + (1-\alpha) K x_n\)
\(\alpha = 1 – \frac{\Delta t}{T}\)
Excelでは次のように設定します。
- C5
\(\Delta t\)を入力します。 - A列
時間 \(t(n\Delta t)\)を入力します。
上の行の値 + \(\Delta t\) - B列
入力値を入力します。
この場合、601秒に0から1に変わります。 - C列
7行目は時定数\(T\)を入力し、9行目で\(\alpha\)を計算します。
11行目に\(K\)、13行目以下に出力の計算式を入力します。